Question

ПОМОГИТЕ, ГЕОМЕТРИЯ.
​

Answer 1

Рассмотрим осевое сечение пирамиды, совпадающее с высотой полученного сечения.

Имеем прямоугольный треугольник, один катет которого равен половине высоты, то есть Н/2, Второй катет равен (1/3) части высоты основания h.

Примем сторону основания за а.

h = a√3/2,   (1/3)h = a√3/6.

Тогда (Н/2) / (a√3/6) = tg α.

Отсюда определяем а = 3Н / (√3tg α) = H√3/tg α.

Площадь основания So = a²√3/4 = 3H²√3/(4tg² α).

Теперь можно получить ответ:

V = (1/3)SoH = (1/3)(3H²√3/(4tg² α))*H = H³√3/(4tg² α).

Answer 2

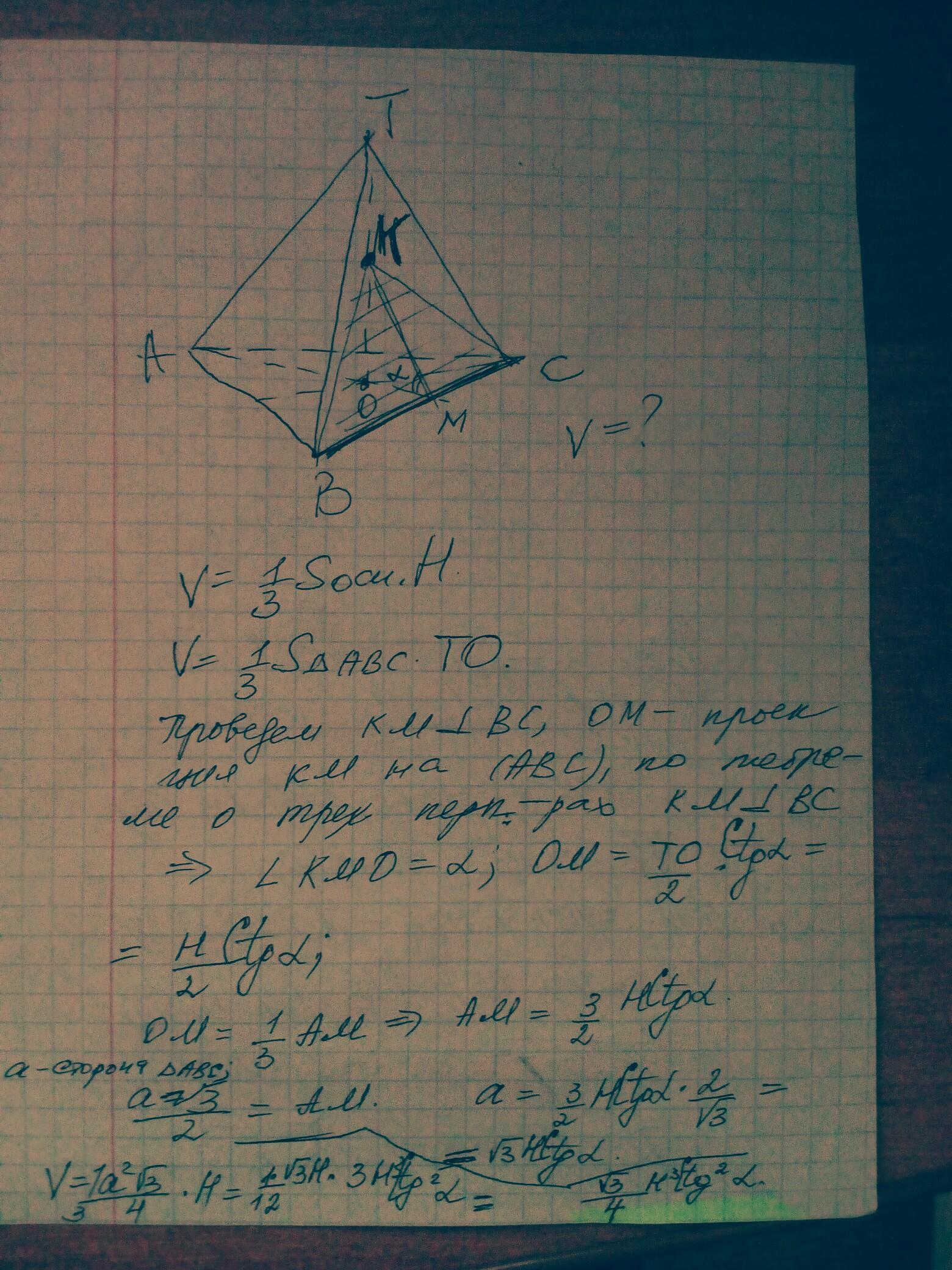
Ответ: во вложении Пошаговое объяснение: