Предмет: Геометрия,
автор: milenaivanishina25
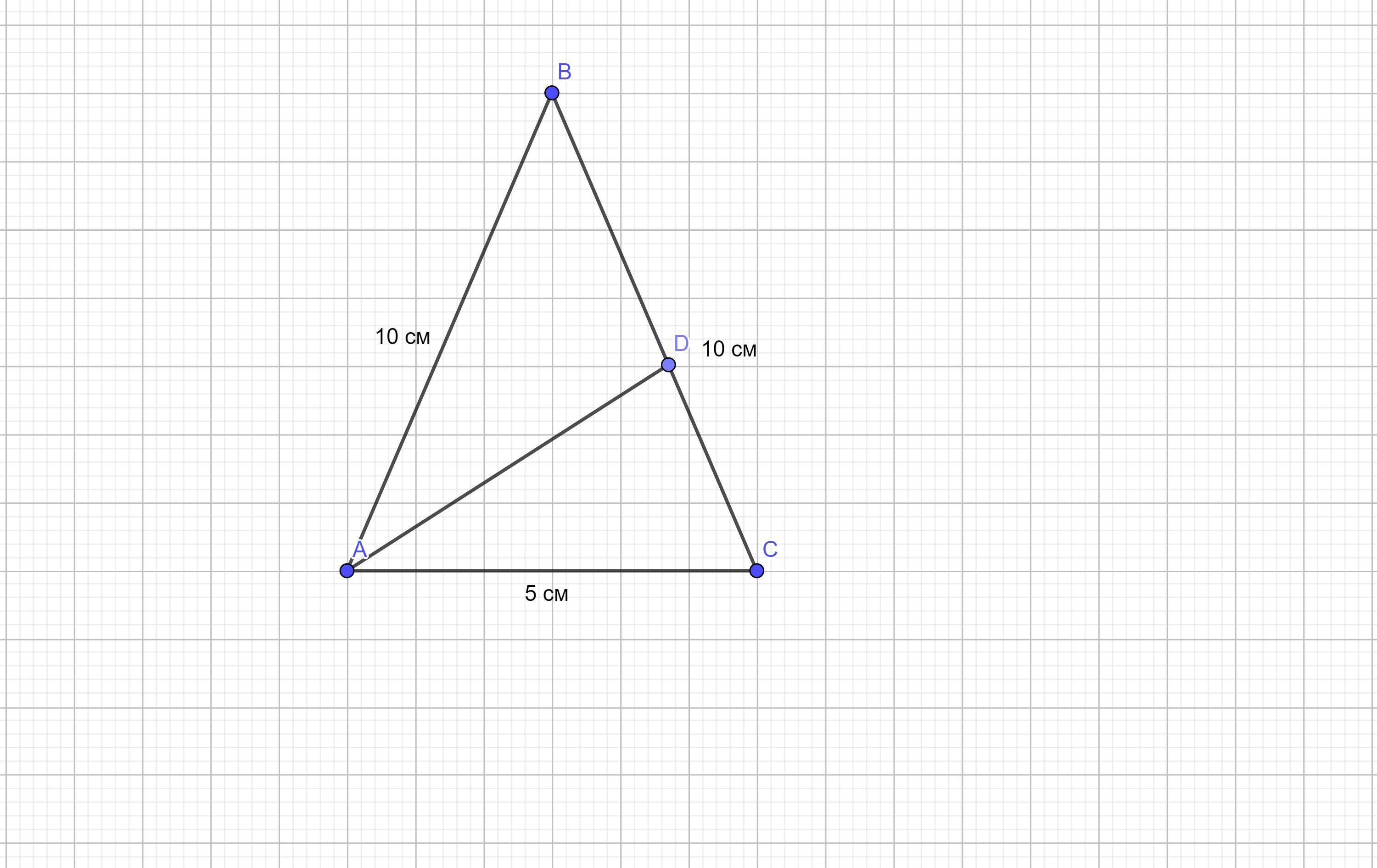
В равнобедренном треугольнике АВС основание АС и боковая сторона АВ соответственно
равны 5 см и 10 см. Биссектриса AD угла А при основании треугольника делит сторону ВС на
отрезки ВD и DС. Найдите длины этих отрезков.
Ответы
Автор ответа:
116
Ответ:
BD = см; CD=
см.
Объяснение:
В ΔABC AB=DC=10 см , AC=5 см , AD - биссектриса.
По свойству биссектрисы треугольника:
Пусть BD = x cм. Тогда CD= 10-x см .
BD = см
CD= 10 - см.
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: sofi1428
Предмет: Русский язык,
автор: lena8494493
Предмет: Английский язык,
автор: aizhanmakhanova22
Предмет: Алгебра,
автор: alom777
Предмет: Алгебра,
автор: SalmanAxe