Предмет: Геометрия,
автор: sholpanmuratali
отрезрк ав расположен вне плоскости а по одну сторону от нее. расстояние от точек а и в до плоскости равны 10 и 14. найдите расстояние от середины отрезка ав до плоскости альфа
Ответы
Автор ответа:
8
Ответ:
12
Объяснение:
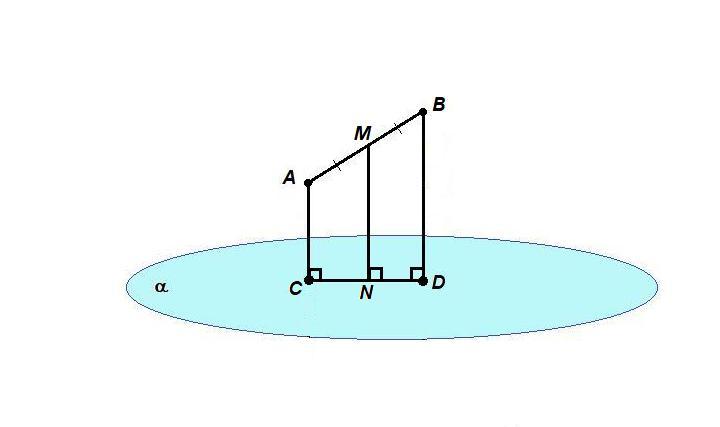
Пусть М - середина отрезка АВ.
Расстояние от точки до плоскости - длина перпендикуляра, опущенного из точки к плоскости.
Проведем АС⊥α, MN⊥α и BD⊥α.
АС = 10,
BD = 14,
MN - искомое расстояние.
Перпендикуляры к одной плоскости параллельны:
АС ║ BD ║ MN
Тогда параллельные прямые АС и BD задают плоскость. Отрезок АВ и точка М лежат в этой плоскости. Тогда и отрезок MN, параллельный АС и BD, так же лежит в этой плоскости.
ACDB - прямоугольная трапеция, MN - ее средняя линия, равна полусумме оснований:
MN = (AC + BD)/2 = (10 + 14)/2 = 12
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: osvitaukotg
Предмет: Математика,
автор: nastacmyr6
Предмет: Английский язык,
автор: nazarlabyk
Предмет: Геометрия,
автор: лера1550
Предмет: Математика,
автор: miXXXtape