Предмет: Алгебра,
автор: alinav2019
Нужно срочно! Решите пожалуйста систему
Приложения:
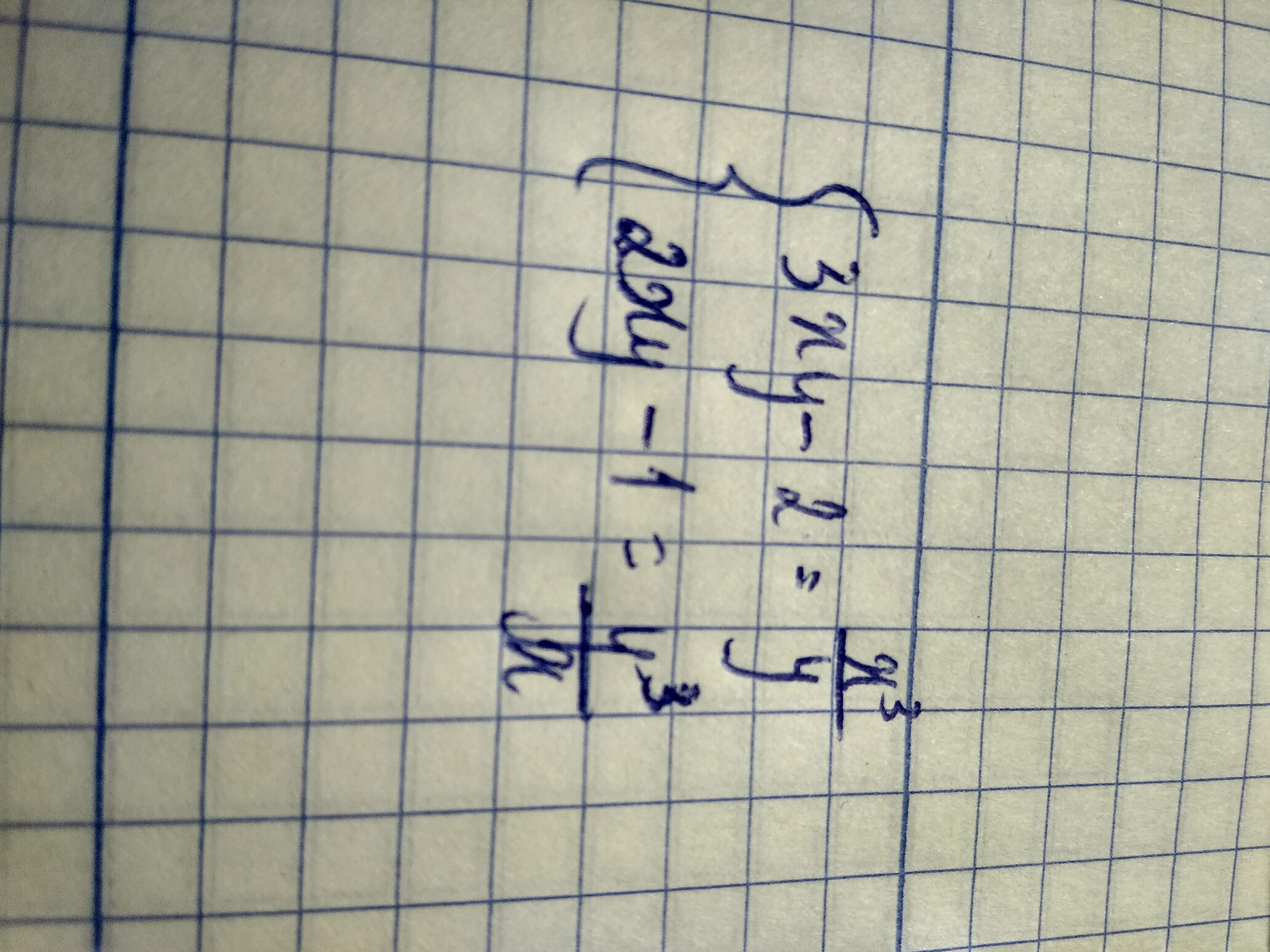
Ответы
Автор ответа:
0
y ∈ ∅
Автор ответа:
0
Відповідь:
Пояснення:
Приложения:

Похожие вопросы
Предмет: Английский язык,
автор: irochkasachenko
Предмет: Українська мова,
автор: asozonuk666
Предмет: Немецкий язык,
автор: dimakolesnik04
Предмет: Математика,
автор: 1939171