Предмет: Алгебра,
автор: Soawii
Найдите область определения функции (любой из трех) с решением
Приложения:
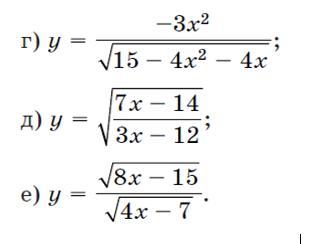
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Область определения данных функций складывается из
неотрицательности подкоренной функции
и неравенства нулю знаменателя
Похожие вопросы
Предмет: История,
автор: egoomnovagooydya
Предмет: История,
автор: egoomnovagooydya
Предмет: Математика,
автор: Bmergut
Предмет: Алгебра,
автор: mariia2001pavlova
Предмет: Биология,
автор: Борисанискевич