Предмет: Геометрия,
автор: 1111119980
точки M,N,K являются серединами сторон треугольника ABC. Зная,что AM=6 см,BN=7см и периметр треугольника ABC равен 36 см,найдите периметр четырехугольника AMNK.
Приложения:
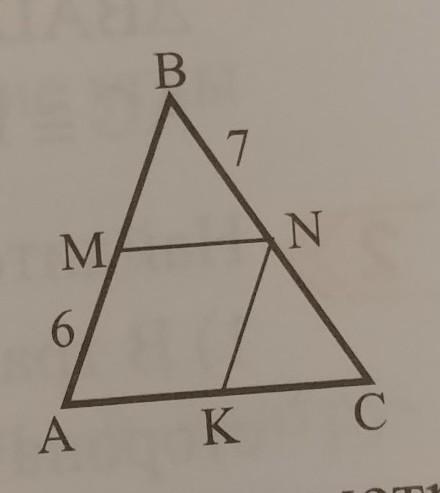
Ответы
Автор ответа:
7
Ответ:
22 см.
Объяснение:
Дано: ΔАВС.
АМ = МВ; BN = NC; AK = KC.
AM = 6 см; BN = 7 см.
Р (ΔАВС) = 36 см.
Найти: P (AMNK)
Решение:
1. Рассмотрим ΔАВС.
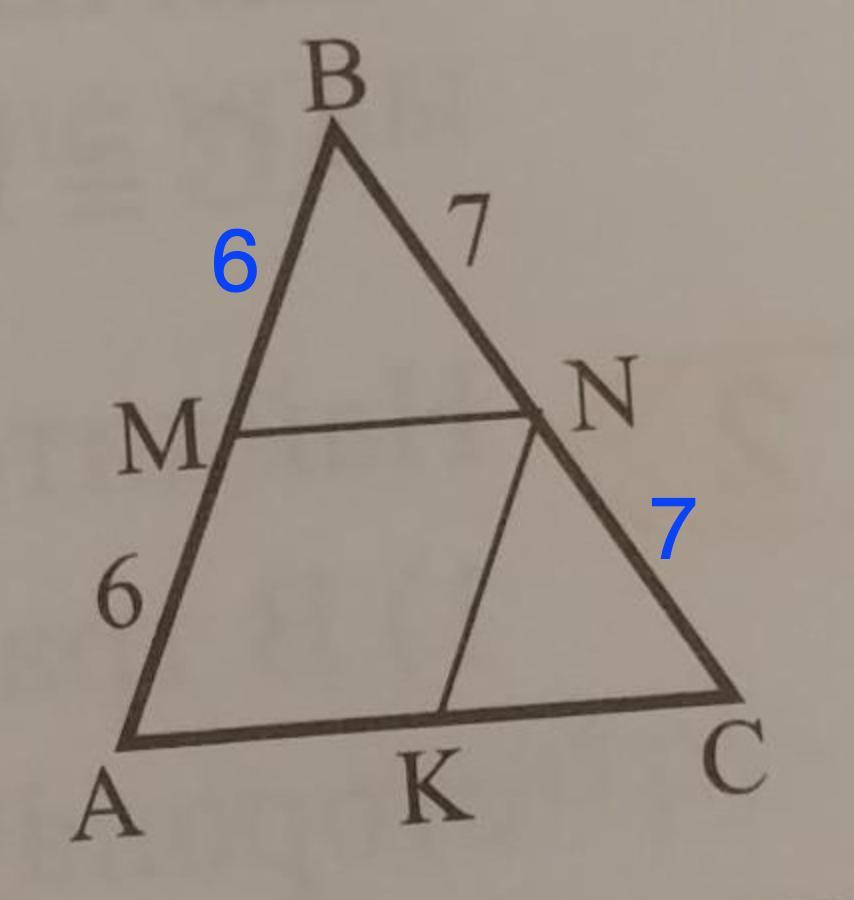
АМ = МВ = 6 см; BN = NC = 7 см (по условию)
⇒АВ = 12 см; ВС = 14 см
Р (ΔАВС) = 36 см
- Периметр - сумма длин всех сторон треугольника.
⇒ АС = 36 - (12+14) = 10 (см)
2. Рассмотрим AMNK.
MN - средняя линия ΔАВС (по условию)
NK - средняя линия ΔАВС (по условию)
- Средняя линия треугольника параллельна основанию и равна его половине.
⇒ MN || AC; KN || AB
⇒ MNKA - параллелограмм (по определению).
- В параллелограмме противоположные стороны равны.
⇒ АМ = NK = 6 см;
MN = AK = 10 : 2 = 5 (см)
- Периметр параллелограмма равен удвоенной сумме смежных сторон.
⇒ Р (AMNK) = 2·(АК + АМ) = 2·(5 + 6) = 22 (см)
Приложения:
Похожие вопросы
Предмет: Биология,
автор: susnikol72
Предмет: Обществознание,
автор: Janais
Предмет: Математика,
автор: davlatovmurat09
Предмет: Математика,
автор: zhunusova1