Предмет: Геометрия,
автор: xaxa123321123321
Через кінець радіуса кулі проведено площину, яка утворює з цим радіусом кут 60 градусів. Знайти радіус кулі , якщо площа перерізу кулі цією площиною = 9п см
НУЖЕН РИСУНОК И ПОЛНОЕ РЕШЕНИЕ
Ответы
Автор ответа:
16
Відповідь:
6 cm
Пояснення:
Переріз кулі будь-якою площиною є кругом, і задача перетворюється на планіметричну.
Площа круга .
Підставляємо S у формулу площі круга:
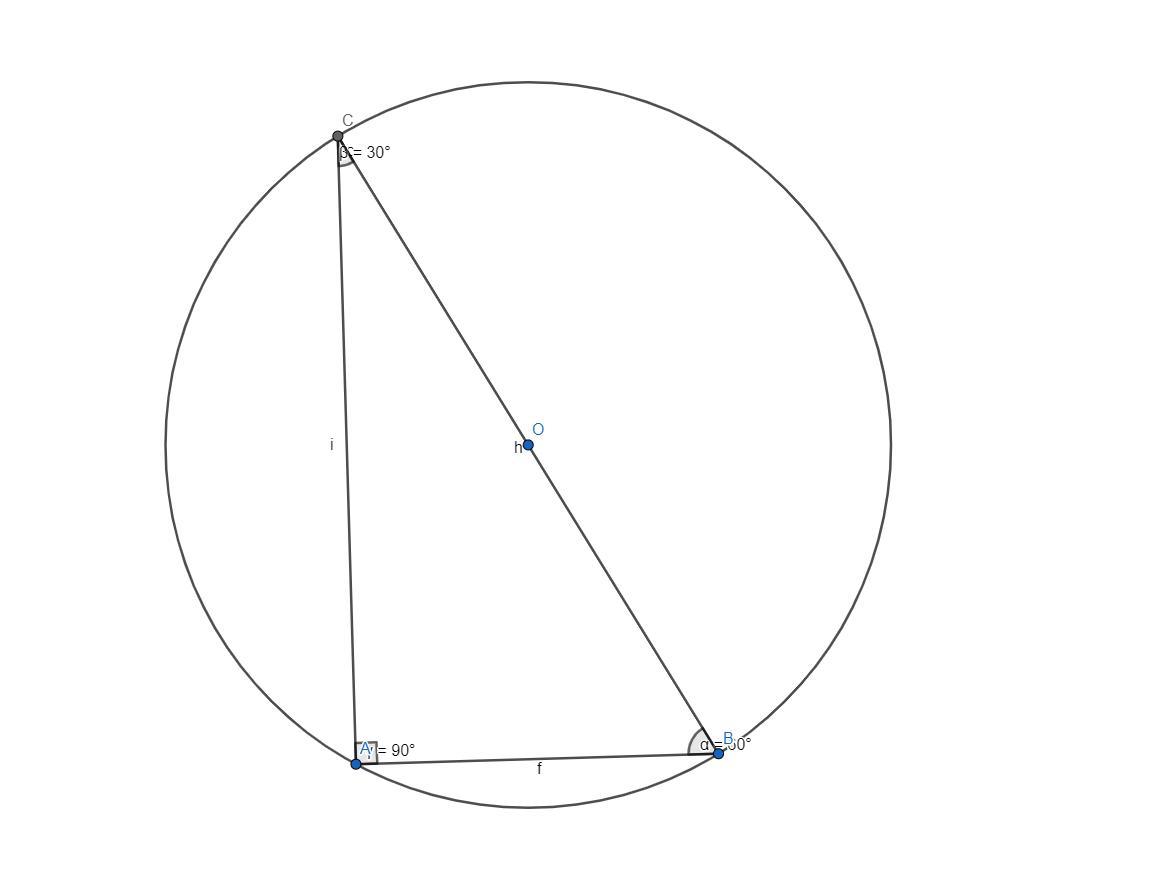
△ABC - прямокутний (CB - діаметр, усі точки лежать на колі), тоді
∠A = 90°
∠B = 60° (за умовою),
а ∠C = 180° - 90° - 60° = 30°
З △ABC:
Приложения:
Похожие вопросы
Предмет: Физика,
автор: Аноним
Предмет: Математика,
автор: valeriastepanova352
Предмет: Информатика,
автор: alyadom
Предмет: Алгебра,
автор: DIvice11
Предмет: Химия,
автор: Amateur22