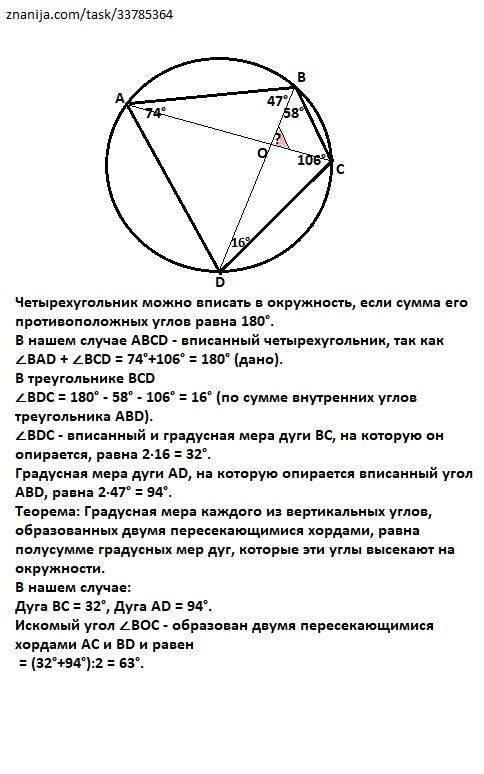
В четырёхугольнике ABCD угол BAD=74 , угол BCD =106 , , угол ABD = 47 , угол CBD = 58. Найдите угол между диагоналями четырёхугольна , противолежащей стороне BC
Ответы
Ответ:
∠ВОС = 63°.
Объяснение:
Пусть точка О - точка пересечения диагоналей четырехугольника.
Четырехугольник можно вписать в окружность, если сумма его противоположных углов равна 180°.
В нашем случае АВСD - вписанный четырехугольник, так как ∠ВАD + ∠ВСD = 74°+106° = 180° (дано).
В треугольнике ВСD
∠BDС = 180° - 58° - 106° = 16° (по сумме внутренних углов треугольника ABD).
∠BDС - вписанный и градусная мера дуги ВС, на которую он опирается, равна 2·16 = 32°.
Градусная мера дуги AD, на которую опирается вписанный угол ABD, равна 2·47° = 94°.
Теорема: Градусная мера каждого из вертикальных углов, образованных двумя пересекающимися хордами, равна полусумме градусных мер дуг, которые эти углы высекают на окружности.
В нашем случае:
Дуга ВС = 32°, Дуга AD = 94°.
Искомый угол ∠BОС - образован двумя пересекающимися хордами АС и BD и равен
= (32°+94°):2 = 63°.