Предмет: Геометрия,
автор: YanaShov
СРОЧНО ПОЖАЛУЙСТА
Треугольник — АВС равнобедренный с основанием .На лучах СА, АВ и ВС, и отмечены соответственно точки D,E и F, и так, что AC=AD, BE=BA, CF=CB. Найдите величину угла BEC, если ∠BDA=25∘, ∠CFA=31∘.
Приложения:
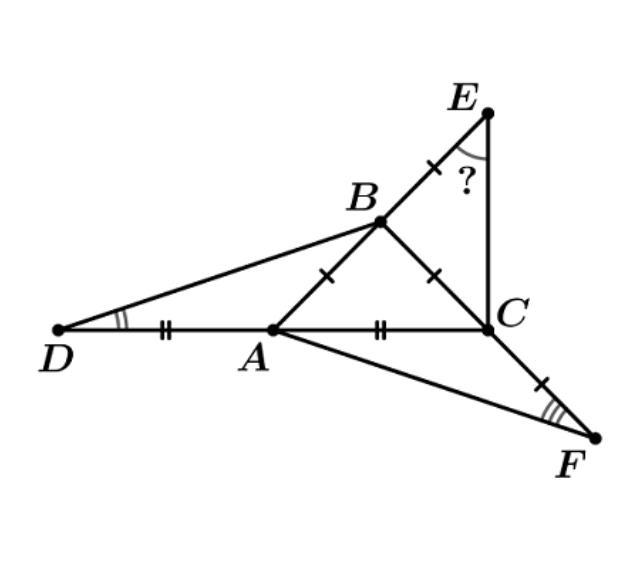
Ответы
Автор ответа:
10
Ответ:
∠ВЕС = 34°.
Объяснение:
Треугольник АВС - равнобедренный. (АВ=ВС) => (∠BAC = ∠BCA).
Тогда ∠DAB = ∠ACF равны как смежные с равными углами.
Треугольники ABD и FCF равны по двум сторонам (AD=AC, AB=CF) и углу между ними (∠DAB = ∠ACF).
В равных треугольниках против равных сторон лежат равные углы. Следовательно, ∠DBA = ∠AFC = 31°, а ∠CAF = ∠BDA = 25°.
∠BCA - внешний угол треугольника АСF и равен сумме двух углов, не смежных с ним, то есть ∠BCA = ∠CAF + ∠CFA = 25+31 = 56°.
∠СВЕ - внешний угол треугольника АВС => ∠СВЕ = ∠BAC + ∠BCA.
∠СВЕ = 56+ 56 = 112°.
Треугольник СВЕ равнобедренный и ∠ВЕС = ∠ЕСВ = (180 - 112/2 = 34° по сумме углов треугольника.
Ответ: ∠ВЕС = 34°.
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: zi556gggg
Предмет: Математика,
автор: dariamihajlisina666
Предмет: География,
автор: kirillblagodarnov
Предмет: Математика,
автор: милан24
Предмет: Физика,
автор: мер13