Предмет: Алгебра,
автор: FlyToMoon228
При каких значениях a и b многочлен M(x) делится без остатка на многочлен:
20 баллов
Приложения:
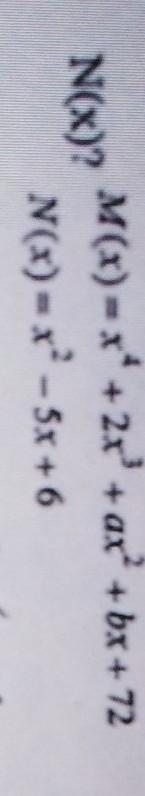
Ответы
Автор ответа:
1
M(x) = x^4 + 2x^3 + ax^2 + bx + 72
N(x) = x^2 - 5x + 6 = (x - 2)(x - 3)
если один многочлен делится без остатка на другой, то корни одного многочлена, являются корнями делимого многочлена
корни второго 2 и 3
значит и корни первого 2 и 3
2^4 + 2*2^3 + a*2^2 + b*2 + 72 = 0
16 + 16 + 4a + 2b + 72 = 0
2a + b = -52
3^4 + 2*3^3 + a*3^2 + b*3 + 72 = 0
81 + 54 + 9a + 3b + 72 = 0
3a + b = - 69
3a + b - 2a - b = -69 + 52
a = -17
2*(-17) + b = -52
b = -18
ответ a=-17 b=-18
-------
ну можно в столбик разделить, зная что если первый многочлен x^2 -5x + 7 то второй будет (смотрим на первый и свободный члены) типа x^2 + cx + 7 и найти эту c
Похожие вопросы
Предмет: Алгебра,
автор: amouser228
Предмет: Алгебра,
автор: Tanjiro4444
Предмет: Химия,
автор: koselevegor968
Предмет: Литература,
автор: Аноним