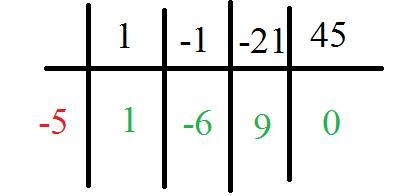Найдите разложения многочленов f(x) и g(x) на неприводимые множители над полями Q, R, C.
f(x) = 4(x + 5)(x + 6)(x + 10)(x + 12) − 3x
^2
;
g(x) = x^3 − x
^2 − 21x + 45.
Это задание как решить? Помогите пожалуйста
Ответы
Ответ:
1) на множестве R и С:
На множестве Q:
.
2) на множестве Q, R и С:
g(x)=(x-3)²(x+5)
Объяснение:
чтобы разложить многочлен axⁿ+bxⁿ⁻¹+cxⁿ⁻2+... на множители, нужно найти его нули и записать разложение в виде: a(x-x₁)(x-x₂)(x-x₃)..., где x₁, x₂, x₃, .... - корни (нули) многочлена.
перемножим почленно 1 скобку с 4-й, а 2-ю с 3-й:
Разделим всё уравнение на x²
Делаем замену:
Тогда
Обратная замена:
Разложение на множестве R и C будет следующим:
2) корни x₃ и x₄ не являются рациональными (нельзя представить в виде обыкновенной дроби), тогда
И разложение на множестве Q будет выглядеть:
.
2) Теперь разбираемся со вторым многочленом:
Находим рациональный корень по схеме Горнера.
Путем перебора делителей свободного члена (числа 45) получаем x₁=-5 (см. рисунок)
Таким образом разложение на Q, R и C будет:
g(x)=(x-3)²(x+5)