Предмет: Алгебра,
автор: Аноним
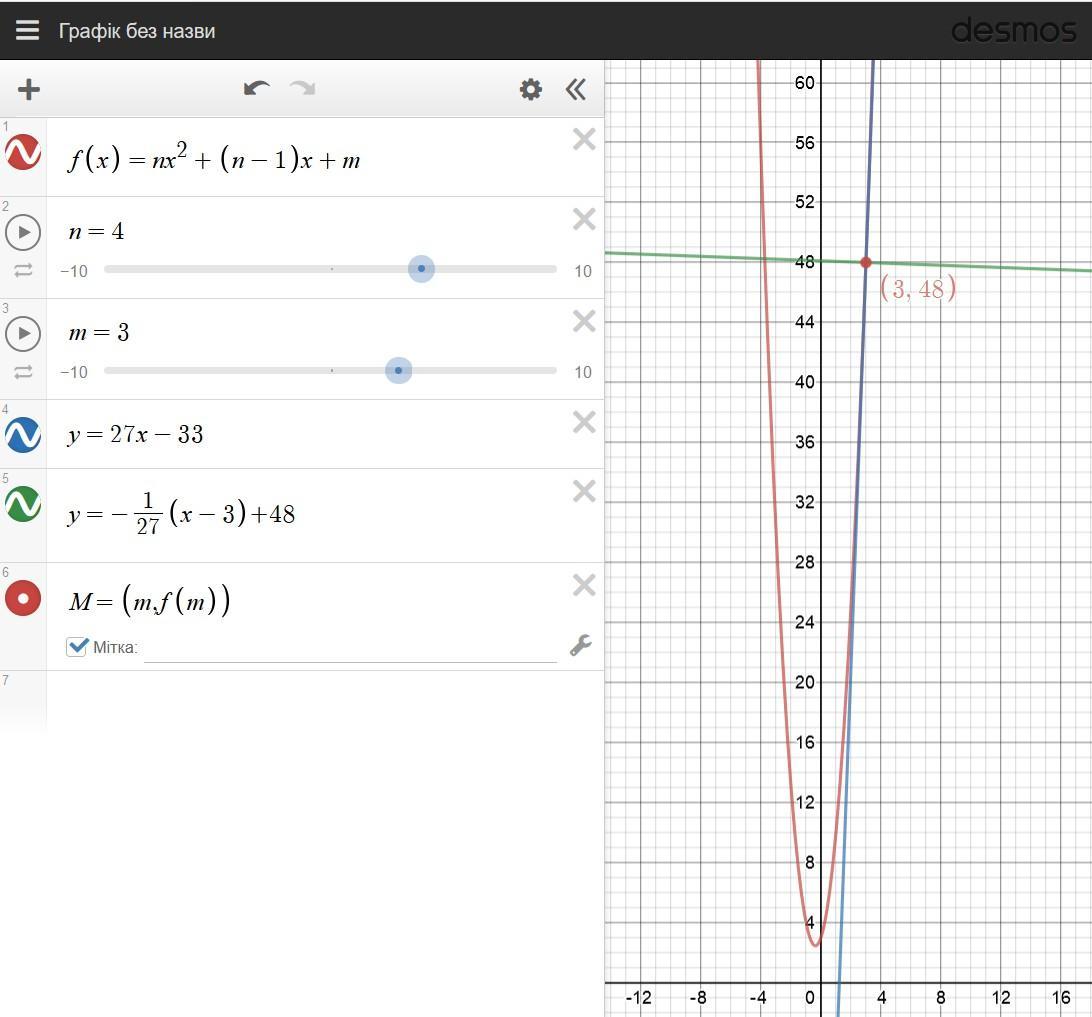
Составить уравнение касательной и нормали к параболе в точке x0=m
y=nx^2+(n-1)x+m
m=3
n=4
Ответы
Автор ответа:
2
Подставим в уравнение параболы значения параметров:
Найдём значение функции в точке :
Найдём производную в точке x₀:
Уравнение касательной имеет вид:
Уравнение нормали имеет вид:
Ответ.
Касательная:
Нормаль:
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Физика,
автор: nnurdinovann
Предмет: Английский язык,
автор: annakurkova05
Предмет: Математика,
автор: влад27111