Предмет: Математика,
автор: matematikL
Исследовать на сходимость ряд
Приложения:
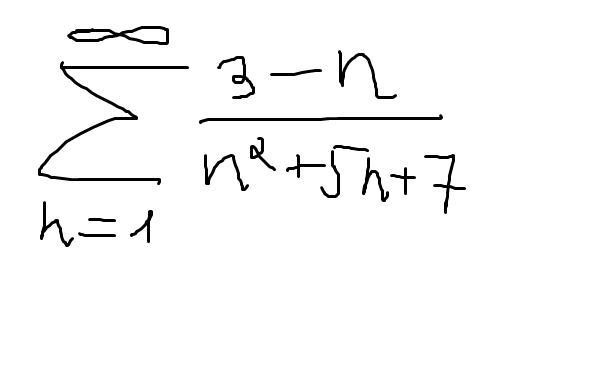
matematikL:
можно просто сказать какой признак использывать
просто если за тп2 тогда выходить -1 и я не знаю что делать
Это не признак, это просто теорема про сходимость ряда
я знаю
необходимое условие сходимости
Ответы
Автор ответа:
1
- гармонический ряд, он расходится. Тогда, по признаку сравнения, расходится и ряд
. Добавление к ряду конечного числа конечных членов не влияет на его сходимость, а значит и исходный ряд расходится
просто нужно было сделать замену и сделать 2 ряда я понял спасибо
я изначально использовал признак сравнения и виходила -1 поэтому я не понимал что делать
Похожие вопросы
Предмет: Математика,
автор: kiriltopikaz
Предмет: Английский язык,
автор: poliiiiiinaaaaaaaaaa
Предмет: Математика,
автор: vlasovaanna20123008
Предмет: Математика,
автор: Аня666777888999
Предмет: Алгебра,
автор: Аноним