Предмет: Геометрия,
автор: aaaa969
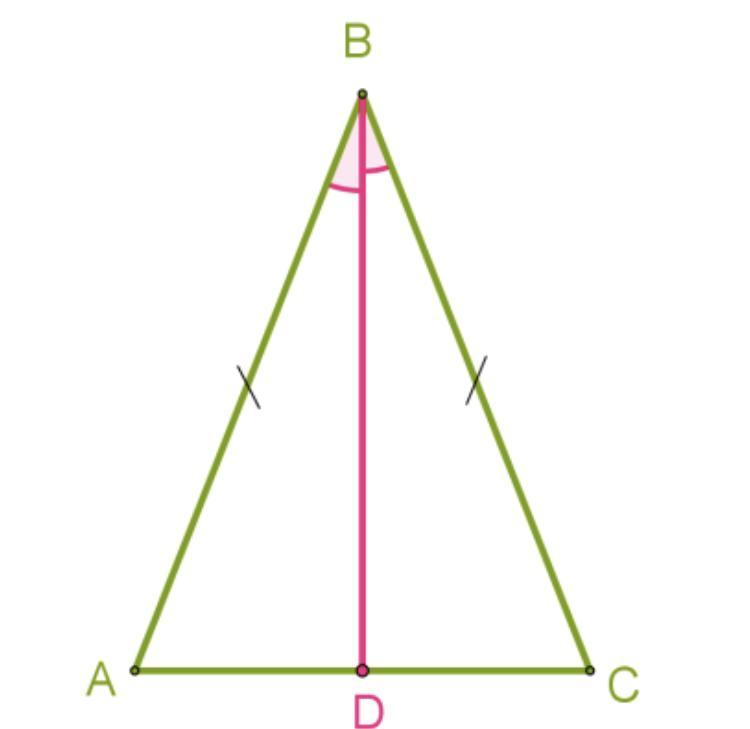
В равнобедренном треугольнике с длиной основания 65 cм проведена биссектриса угла ∡ABC. Используя второй признак равенства треугольников, докажи, что отрезок BD является медианой, и определи длину отрезка AD.
Рассмотрим треугольники ΔABD и Δ (треугольник записать в алфавитном порядке);
1. так как прилежащие к основанию углы данного равнобедренного треугольника равны, то ∡ A = ∡ ;
2. так как проведена биссектриса, то ∡ = ∡ CBD;
3. стороны AB=CB у треугольников ΔABD и ΔCBD равны, так как данный ΔABC — .
По второму признаку равенства треугольников ΔABD и ΔCBD равны.
Значит, равны все соответствующие элементы, в том числе стороны AD=CD. А это означает, что отрезок BD является медианой данного треугольника и делит сторону AC пополам.
AD= см.
ПОМОГИТЕ ПОЖАЛУЙСТА!!!
Приложения:
Ответы
Автор ответа:
18
Ответ:
Равнобедренный треугольник.
Приложения:

Pyatachok735:
Помогите пожалуйста - https://znanija.com/task/33776114
Похожие вопросы
Предмет: Физика,
автор: dsfsdfsdfsdfsd18
Предмет: Русский язык,
автор: diandi8243
Предмет: Литература,
автор: aminaamina4565
Предмет: Физика,
автор: Vika6698
Предмет: Математика,
автор: Аноним