Предмет: Геометрия,
автор: stasik0907
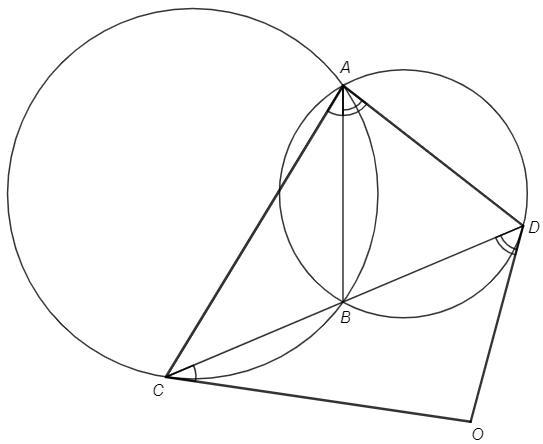
Помогите! Две окружности пересекаются в точках А и В. Через точку В проведена прямая, пересекающая окружности в точках С и D. Каcательные к окружностям, проведенные через точки С и D, пересекаются в точке О. Докажите, что около четырехугольника АCOD можно описать окружность.
Ответы
Автор ответа:
2
BCO =∪BC/2 (угол между касательной и хордой)
BAC =∪BC/2 (вписанный угол)
BCO =BAC
Аналогично BDO=BAD
BCO+BDO +O =180 => BAC+BAD +O =180 => CAD+O =180
ACOD - вписанный четырехугольник, т.к. сумма его противоположных углов 180.
Приложения:
Похожие вопросы
Предмет: Химия,
автор: polyakova290305
Предмет: Математика,
автор: 79wu
Предмет: Математика,
автор: natalija2012
Предмет: История,
автор: Аноним
Предмет: Химия,
автор: Oksaniti