Предмет: Алгебра,
автор: MuwikGramm
Найти предел БЕЗ правила Лопиталя.
Приложения:
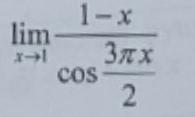
Ответы
Автор ответа:
2
Похожие вопросы
Предмет: География,
автор: gadzieva388
Предмет: Биология,
автор: aishasagangyn
Предмет: Математика,
автор: NickWilson
Предмет: Химия,
автор: Bonne111
Предмет: Литература,
автор: krisour