Предмет: Математика,
автор: HEYGAIS
Кто разбирается в производных, помогите пожалуйста) Надо найти первую производную
Приложения:
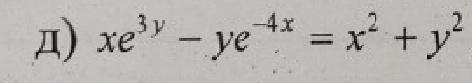
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
деффернцируем в неявном виде левую и правую часть:
Похожие вопросы
Предмет: Окружающий мир,
автор: vladkalishko
Предмет: Физика,
автор: pokaliroma
Предмет: Английский язык,
автор: marishka2637
Предмет: Литература,
автор: луи13