Предмет: Алгебра,
автор: TALUNAOATAT91
Помогите 20 балов все на фото
Приложения:
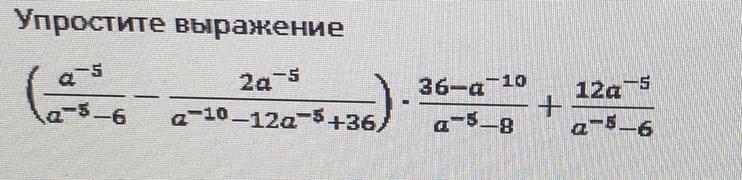
Ответы
Автор ответа:
1
Сделаем замену
Перепишем выражение
Во второй дроби в скобках свернём знаменатель в формулу
Приведем скобки к общему знаменателю
Т.к. у нас выражение в знаменателе под квадратом, то можем поменять местами слагаемые в скобках, получим (6-х)²
Раскрываем скобки в числителе, 36-х² расписываем как (6-х)(6+х), затем сокращаем со знаменателем выражения из скобок.
Сокращаем
Выносим минус из второй дроби, получили общий знаменатель, переписываем как одну дробь
Делаем обратную замену
Похожие вопросы
Предмет: Математика,
автор: fkrkrnejcmendjdnene
Предмет: История,
автор: SvetaNikk
Предмет: Литература,
автор: komarnitsckaoksana81
Предмет: История,
автор: svetachernysho
Предмет: Литература,
автор: Миленаспроси1