Предмет: Алгебра,
автор: Вероника9358
Даю 100 баллов! Срочно!
Решить несобственный интеграл с точкой разрыва x=2
Приложения:
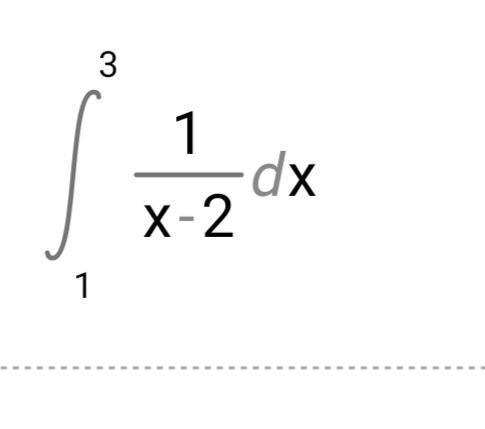
Simba2017:
-ln2
ответ Ln|x-2|
после подстановки ln1-ln1=0
Там точна разрыва, решение неверно
решите вы!
Ответы
Автор ответа:
2
Подынтегральная функция имеет разрыв в точке x = 2.
Как видим неопределенность, интеграл расходится.
так чему он тогда равен, бесконечности?
неопределенности.
и как тут пытаются доказать, что именно, когда заходите в тупик, он и расходится)
Senpai908, надо вам ответ расписать все же до конца....
хотя бы для нас)
по теории пишут, если он расходится , то не существует...
но вспомним геом. смысл интеграла. это площадь. Она же есть, никуда не девалась.) Значит, существует.
по вашему тогда эту площадь не найти
Есть неопределенность это и значит что не определен определённый интеграл.
согласен
Автор ответа:
1
Попытка номер два)))))))))))))))))
Приложения:

Похожие вопросы
Предмет: История,
автор: rinkdiana3
Предмет: Информатика,
автор: dasaureva974
Предмет: Английский язык,
автор: nikitacisnikov79
Предмет: Математика,
автор: Саша748367250438387