Предмет: Математика,
автор: zhenyakuzneczov2001
Помогите пожалуйста Срочно, не через фотомат
Приложения:
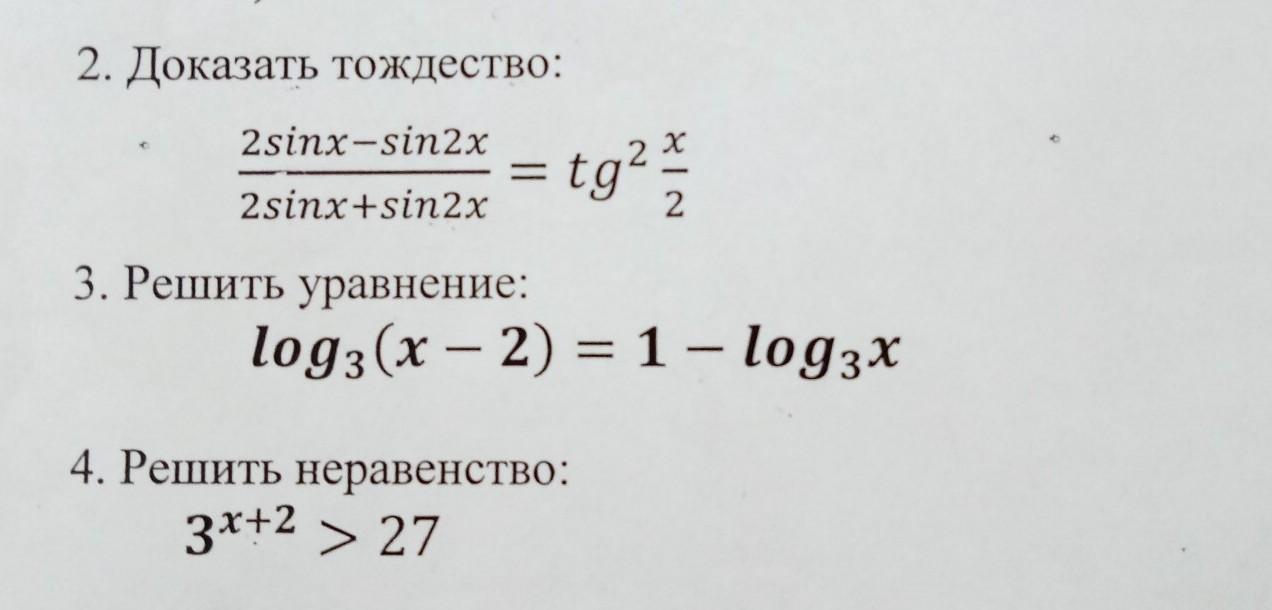
Ответы
Автор ответа:
1
zhenyakuzneczov2001:
спасибо большое
Похожие вопросы
Предмет: Химия,
автор: mstorozhenko1582
Предмет: Алгебра,
автор: rdrediska5922
Предмет: Українська мова,
автор: severun2829
Предмет: Математика,
автор: dvdbgm
Предмет: Математика,
автор: Миша1987