Предмет: Геометрия,
автор: nanannanannana
20 БАЛЛОВ. С ОБЪЯСНЕНИЕМ ПЛС.
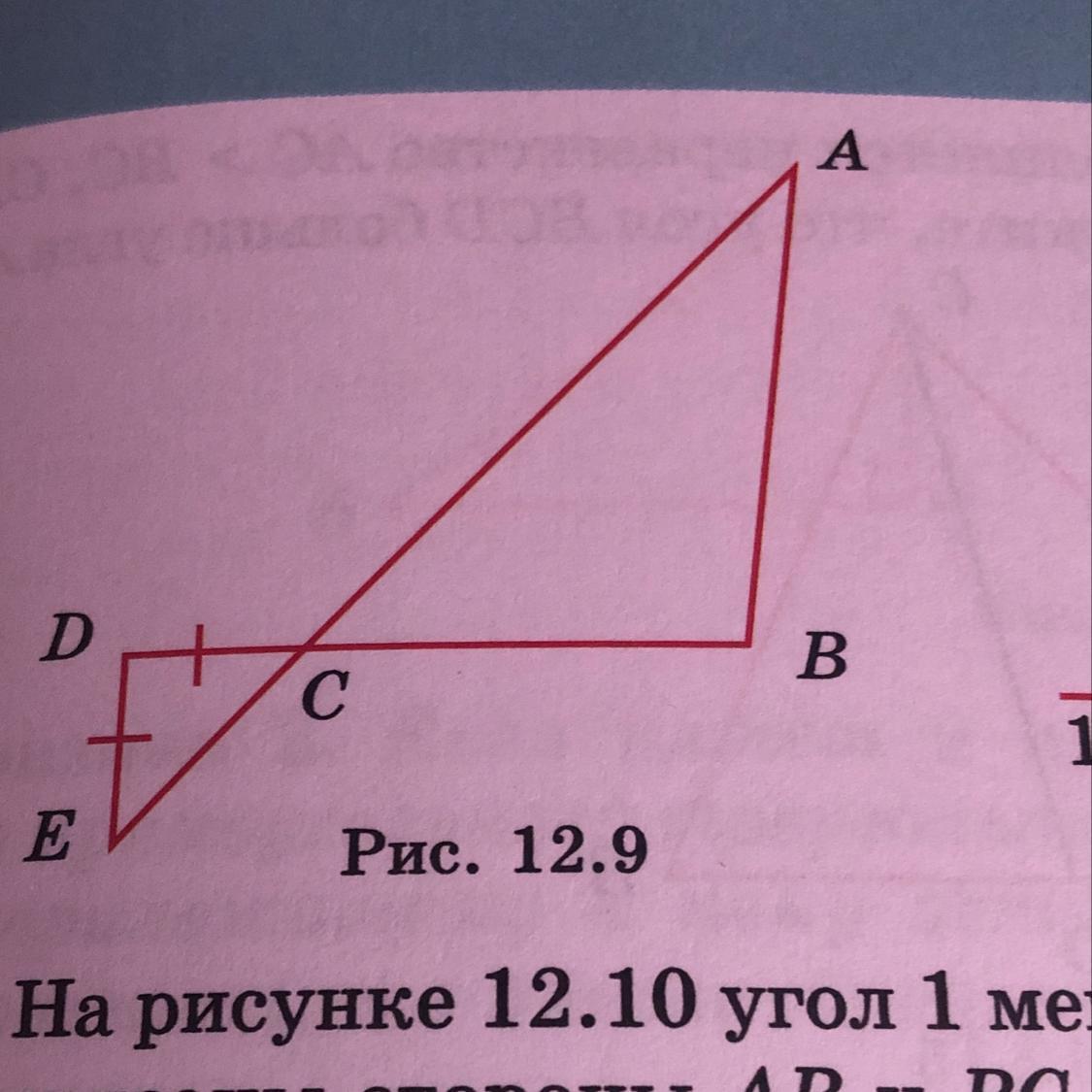
Отрезки АЕ и ВD пересекаются в точке С, АВ>ВС, СD=DE (рис.12.9). Докажите, что угол ВАС меньше угла DEC.
Приложения:
Ответы
Автор ответа:
10
<BAC=<DEC- это выполнялось бы . если треугольники были бы подобны и тогда CB=AB
Но по условию задачи AB>CB, поэтому <BAC≠<DEC
<DEC=<DCE=<ACB(последние 2 угла вертикальные, поэтому равны)
значит надо доказать что в ΔАВС <A меньше <ACB
по т синусов для треугольника АВС
AB/sin<ACB=CB/sin<A
так как AB>BC и синус угла-возрастает от 0 до 90 градусов, то
следует что делитель первой дроби больше делителя второй
Или sin<ACB больше sin<A-значит <ACB больше <A
и <CDE больше <BAC
Simba2017:
нет у вас вопросов без ответов, выставляйте как обычно
Похожие вопросы
Предмет: Математика,
автор: Robin6148
Предмет: Математика,
автор: tertyshnikovad8606
Предмет: Математика,
автор: gelena1324
Предмет: География,
автор: Аноним