Предмет: Математика,
автор: KatherinePirs
Помогите с неопределённым интегралом, пожалуйста
Приложения:
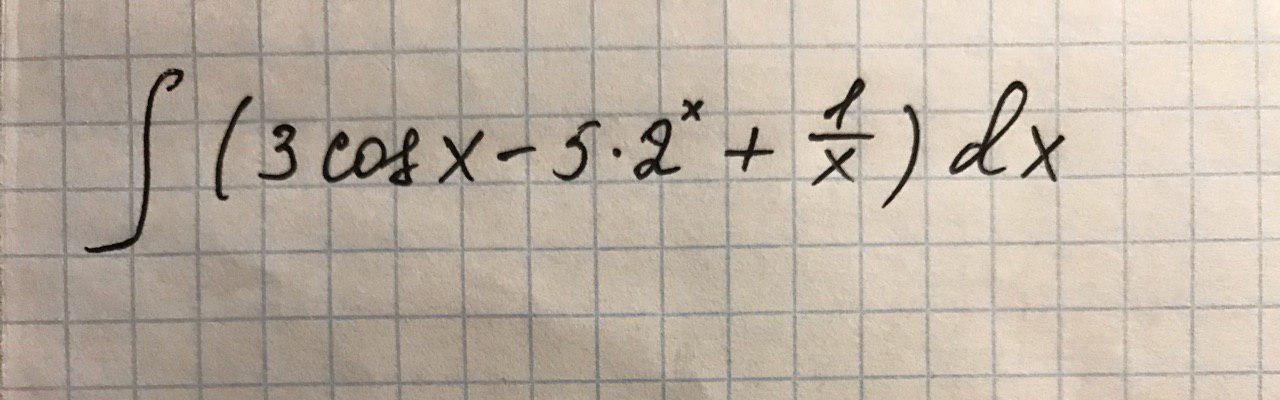
Ответы
Автор ответа:
3
Ответ:
Пошаговое объяснение:
Автор ответа:
1
Вычислить неопределенный интеграл.
Используемые свойства интеграла:
;
, где 'с' независима от 'х'.
Используемые формулы таблицы интегралов:
;
;
.
Похожие вопросы
Предмет: Биология,
автор: zininan6852
Предмет: Информатика,
автор: irinaf9244
Предмет: География,
автор: lizapr2012
Предмет: Математика,
автор: mamochka86