Предмет: Геометрия,
автор: xudaykuliyevatajan
в треугольнике с основанием равным а вписан квадрат,одна из сторон которого лежит на основании треугольника.Площадь квадрата составляет 1/6 часть площади треугольника.Определите высоту треугольника и сторону квадрата.
Ответы
Автор ответа:
2
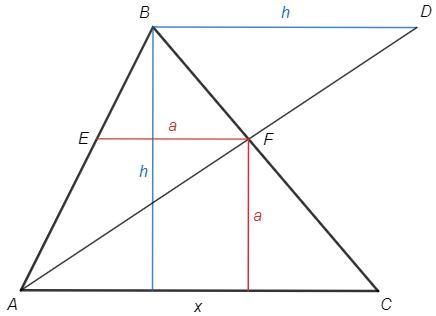
h - высота ABC. Построим BD||AC, BD=h. EF||AC.
Основание треугольника BAD равно его высоте. Треугольники BAD и EAF подобны, их основания относятся как высоты. Основание треугольника EAF равно его высоте. EF - сторона вписанного квадрата, EF=a.
Пусть площадь квадрата меньше площади треугольника в k раз, AC=x, тогда площадь ABC
xh/2 = ka^2
Треугольники AFC и DFB подобны
x/h = a/(h-a)
xh = 2ka^2
x+h = xh/a = 2ka
По теореме Виета
x,h = ka +- V(k^2*a^2 -2ka^2)
x,h = a( k ± √(k(k-2)) )
При k=6
x,h = a(6 +- 2V6)
Приложения:
Похожие вопросы
Предмет: Биология,
автор: cttkbgfd2441
Предмет: География,
автор: annaledi6063
Предмет: Русский язык,
автор: HEIIOSASHA2964
Предмет: Геометрия,
автор: вазя891
Предмет: Математика,
автор: Котенько