Предмет: Математика,
автор: batirgireevasau1
100 БАЛЛОВ
ЛОГАРИФМЫ СИСТЕМА
Приложения:
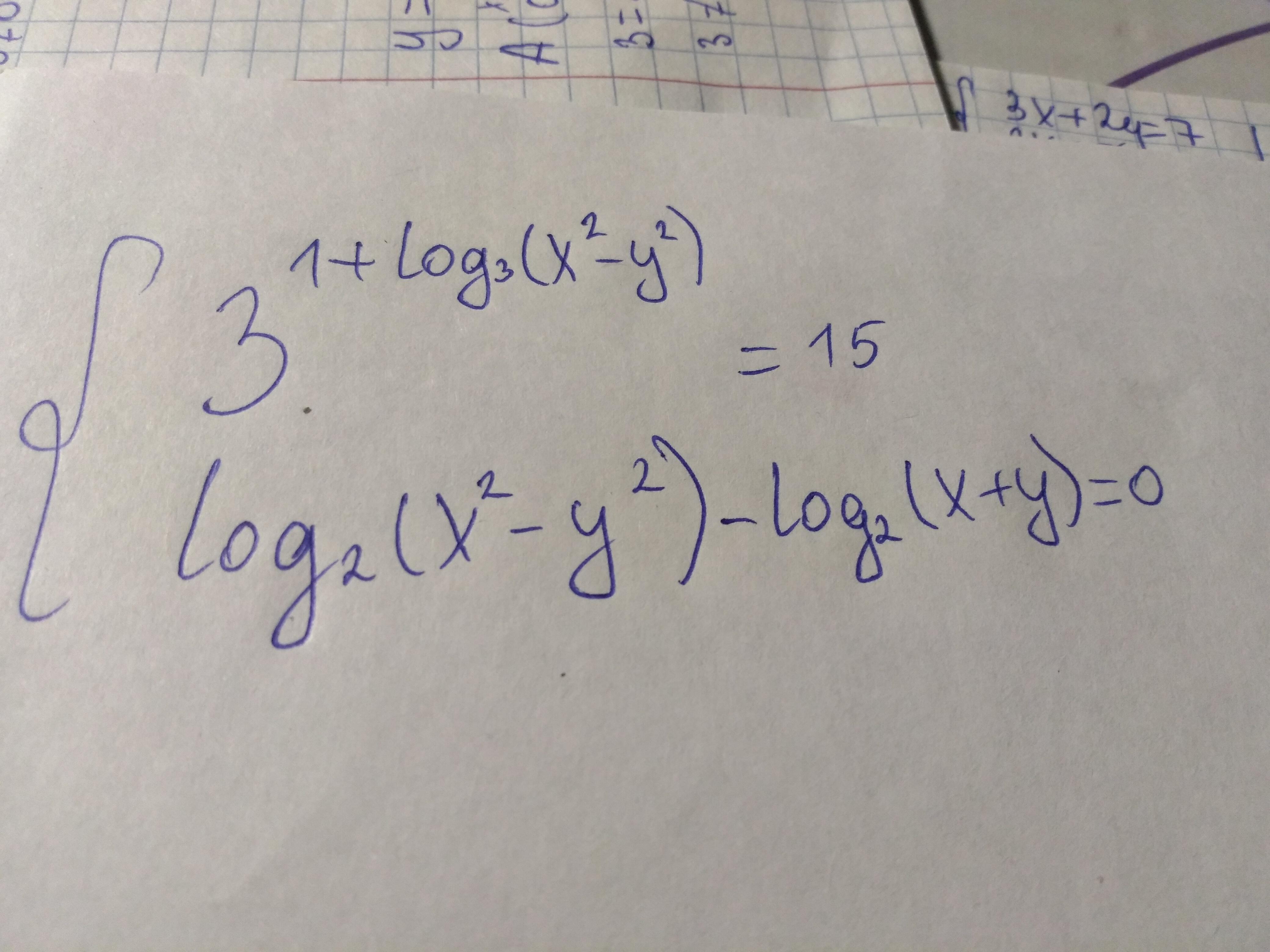
Ответы
Автор ответа:
1
о, наконец то интересные задания. давай считать :)
разберёмся сначала с первым уравнением
теперь со вторым
имеем систему
путём несложных подстановок(благо ситуация в данный момент позволяет их совершить) находим что x = 3, y = 2. проверяем на всякий
batirgireevasau1:
У меня в добавленных
В профиле
мм странно, не вижу. последнее добавленное показывает это задание
Секунду
https://znanija.com/task/337305418
https://znanija.com/task/33730541
1 неправильная ссылка. Га вторую
На*
https://znanija.com/profil/batirgireevasau1-10086843
Короче, на вторую
Похожие вопросы
Предмет: География,
автор: yarexonita
Предмет: Математика,
автор: vrach20211505
Предмет: Математика,
автор: saraev22386
Предмет: Химия,
автор: anastasiyac4