Предмет: Алгебра,
автор: ChristineVI
40БАЛЛОВ
докажи тождество
Приложения:
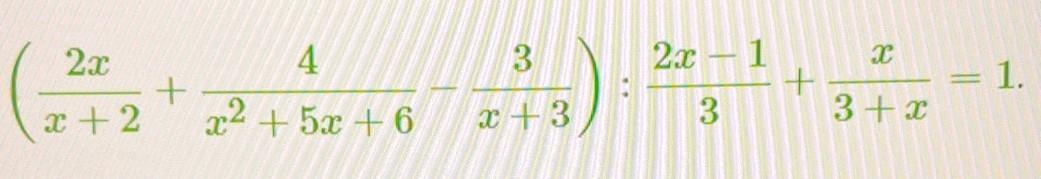
Ответы
Автор ответа:
5
Ответ:
Объяснение:
доказано
Автор ответа:
1
Ответ: во вложении объяснение:
Приложения:

Похожие вопросы
Предмет: Биология,
автор: alexdasha
Предмет: Алгебра,
автор: gruckovskijandrij
Предмет: История,
автор: kararostuk
Предмет: Математика,
автор: njcz1985
Предмет: Литература,
автор: AlinaHvan1