Предмет: Алгебра,
автор: SAFNUR2004
Найдите сумму всех членов бесконечно убывающей геометрической прогрессии
Приложения:
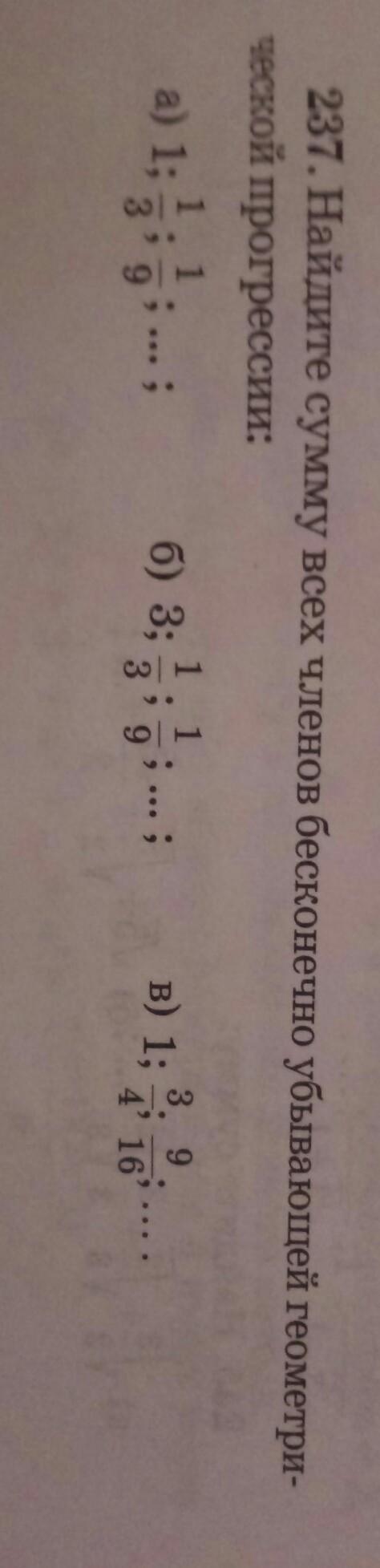
Ответы
Автор ответа:
1
Ответ:
а) 1,5
б) 4,5
в) 4
Объяснение:
а)
б)
В написанном виде прогрессия не является геометрической, т к.
а2/а1 = 1/3 : 3 = 1/9
и не равно
а3/а2 = 1/9 : 1/3 = 1/3
Но если предположить, что пропущен а2, равный единице, получим:
в)
SAFNUR2004:
А б) и в)
Дополнил решение. Внимательнее, пожалуйста, к заданию под буквой "б"!
Похожие вопросы
Предмет: Математика,
автор: namazovfirengiz
Предмет: Українська література,
автор: motrinetsmariua
Предмет: Математика,
автор: isaesenbaev63
Предмет: Математика,
автор: albarpp9