Предмет: Математика,
автор: elftv01
Срочно!!! Решить производную!
Приложения:
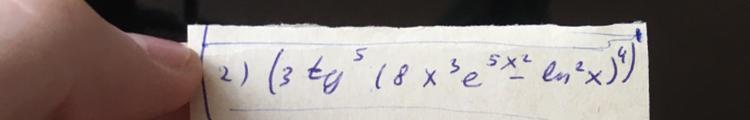
Ответы
Автор ответа:
0
Пошаговое объяснение:
Похожие вопросы
Предмет: Другие предметы,
автор: HirokoCrashxax
Предмет: Литература,
автор: emilianzaverjuhha
Предмет: Литература,
автор: alenaliy5846
Предмет: Математика,
автор: Рушана2016
Предмет: Алгебра,
автор: ksenyarybalko1