Предмет: Геометрия,
автор: lesha132435kartosha
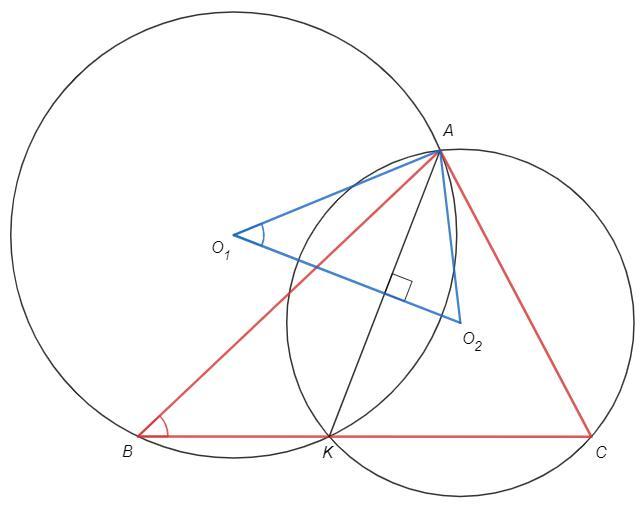
Треугольник разбит на два других треугольника прямой, проведенной из вершины. Доказать что центры кругов описанных около всех трех треуголтников лежат на одной окружности с вершиной
Ответы
Автор ответа:
1
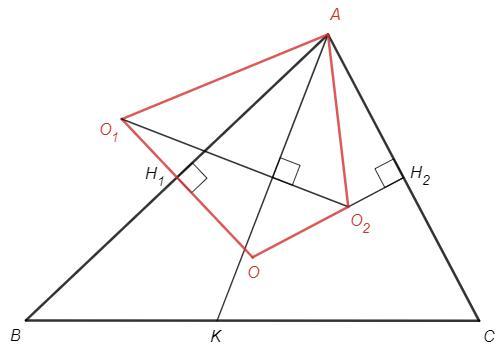
Центр описанной окружности - пересечение серединных перпендикуляров к сторонам.
Линия центров O1O2 перпендикулярна общей хорде AK и делит дугу AK пополам. Центральный угол O1 опирается на половину дуги AK, вписанный угол B опирается на дугу AK, O1=B. Аналогично O2=C => O1AO2=BAC.
В четырехугольнике AH1OH2 сумма противоположных углов H1 и H2 равна 180, следовательно сумма другой пары также 180, H1AH2+O=180.
BAC+O=180 => O1AO2+O=180 => AO1OO2 - вписанный четырехугольник.
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: genkulmaria757
Предмет: Математика,
автор: jjmgd7jsq8
Предмет: Математика,
автор: olabezdosuk
Предмет: География,
автор: Сако54
Предмет: Алгебра,
автор: Аноним