Предмет: Алгебра,
автор: Yourkohai
Решите способом подстановки систему уравнений
Приложения:
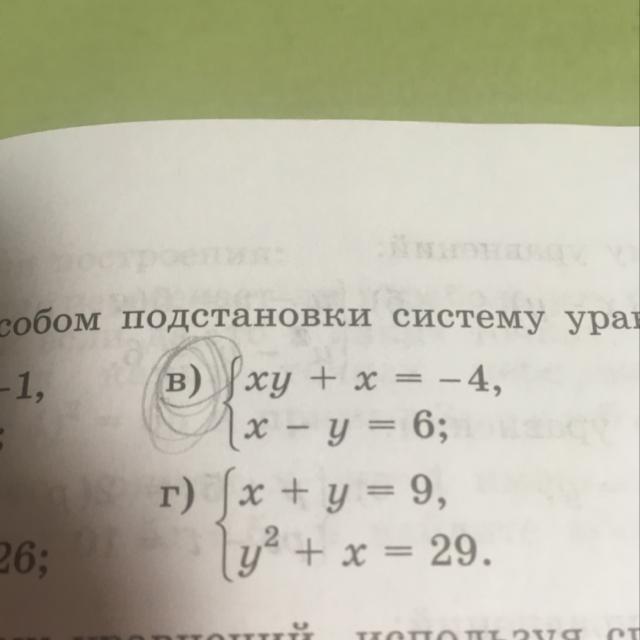
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Геометрия,
автор: Sasha2281337Just
Предмет: История,
автор: artemsereda950
Предмет: Математика,
автор: kaktussikk
Предмет: Биология,
автор: убийца21
Предмет: Литература,
автор: ErasylKSGO