Предмет: Математика,
автор: daun487236857256
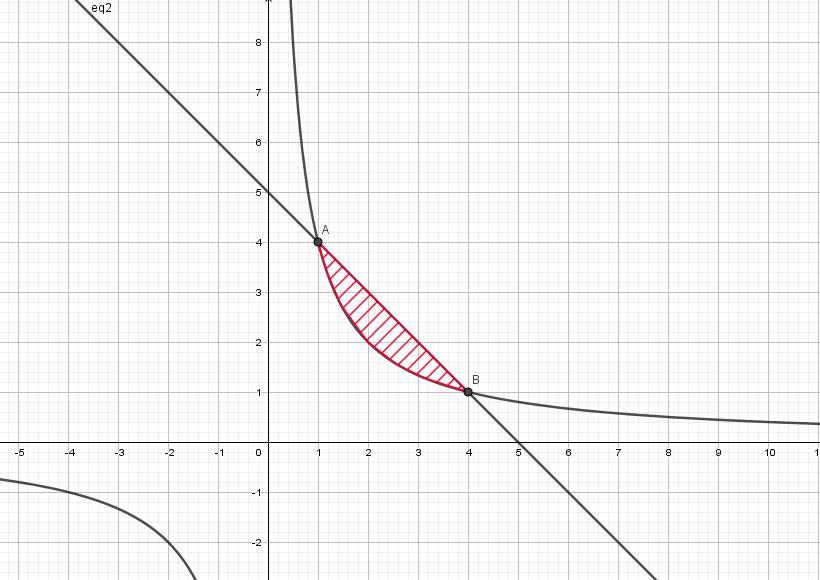
вычислить двойной интеграл ∫∫xy² D: xy=4 , x+y-5=0
Аноним:
441/20 = 22.05
Ответы
Автор ответа:
4
Приложения:
Похожие вопросы
Предмет: Математика,
автор: andreyshlapak2309123
Предмет: Алгебра,
автор: gromblack653
Предмет: Математика,
автор: martovskayakoshechka
Предмет: Математика,
автор: полина1486
Предмет: Математика,
автор: Vovchik20057