Предмет: Математика,
автор: Yanuska11
ПОМОГИТЕ РЕШИТЬ ПОДРОБНО!!!
Приложения:
Ответы
Автор ответа:
1
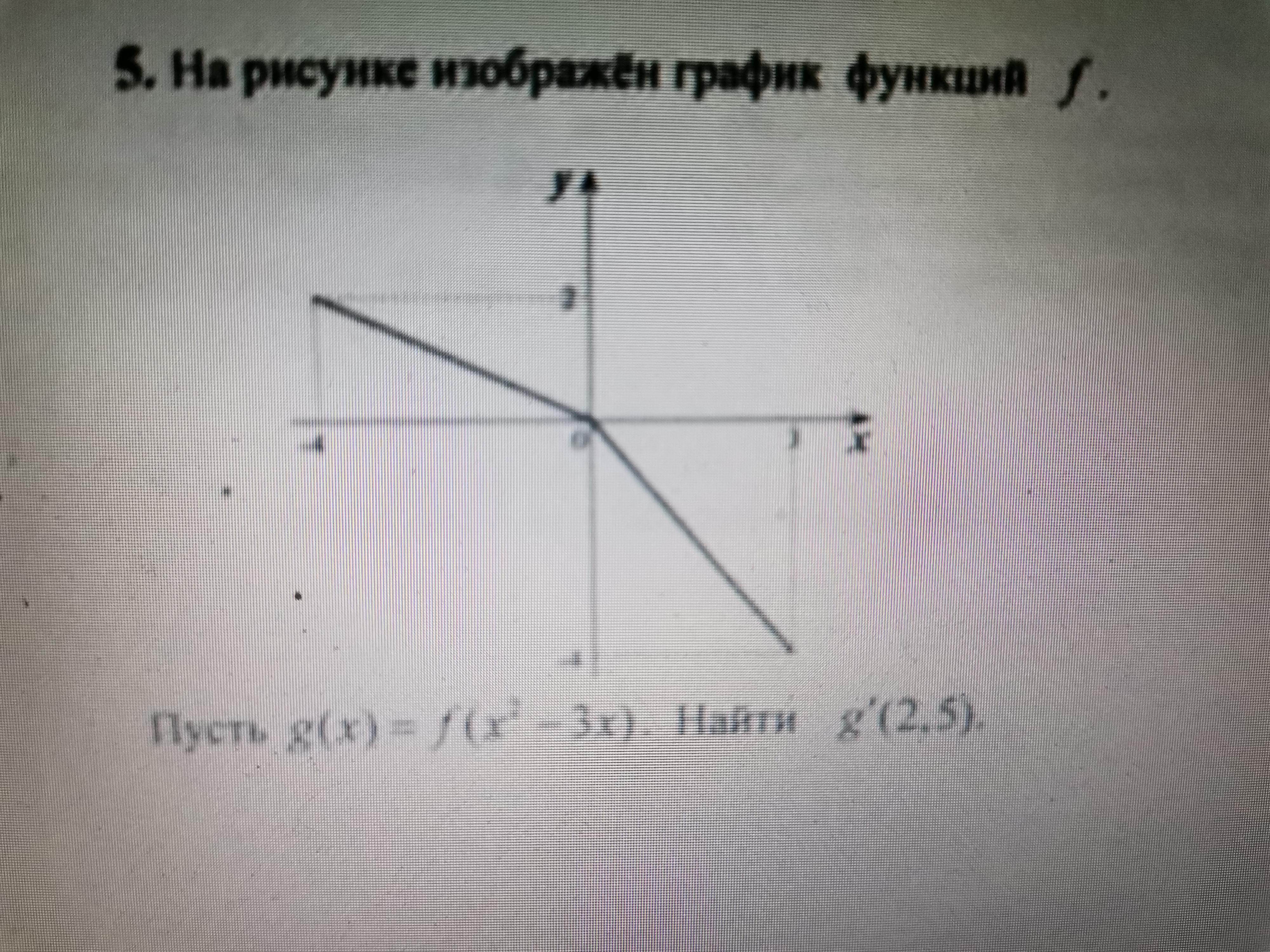
Значит, ; Для
:
; Из рисунка видно, что
- тангенс угла наклона прямой левой части графика.
Итак,
Yanuska11:
А почему производная g' находится именно так? Или здесь, как я понимаю производная функции, умноженная на тангенс?
дело в том, что f(x^2-2x) — сложная функция. соответственно ее производная находится по формуле производной сложной функции
-3х*
Ааа, точно. Спасибо!
Похожие вопросы
Предмет: Математика,
автор: mihailarhypenko
Предмет: Математика,
автор: emiliaignatenko
Предмет: Литература,
автор: nnakorkesko
Предмет: Биология,
автор: crowmen3
Предмет: Литература,
автор: Аноним