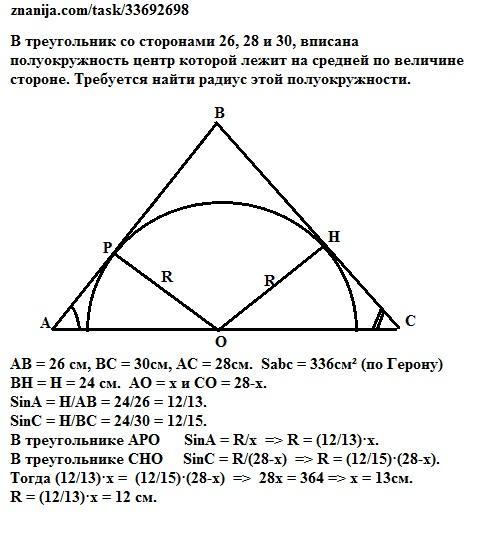
В треугольник со сторонами 26, 28 и 30, вписана полуокружность центр которой лежит на средней по величине стороне. Требуется найти радиус этой полуокружности.
Ответы
Ответ:
R = 12 см.
Объяснение:
Пусть дан треугольник АВС со сторонами АВ=26, ВС=30см и
АС =28 см. Площадь треугольника АВС с полупериметром
р = (26+28+30)/2 = 42 см по формуле Герона:
S = √(42·(42-26)·(42-28)·(42-30)) = 6·2·4·7 = 336 см².
Тогда высота, проведенная к средней по величине стороне, равна:
Н = 2·S/28 = 336/14 = 24 см. =>
SinA = H/AB = 24/26 = 12/13.
SinC = H/BC = 24/30 = 12/15.
Окружность с центром О, расположенным на стороне АС, касается сторон АВ и ВС в точках Р и Н соответственно. Тогда треугольники АРО и СНО - прямоугольные, так как радиусы ОР и ОН перпендикулярны касательным в точках касания.
Пусть точка О делит сторону АС на отрезки АО = х и СО = 28-х.
В треугольнике АРО SinA = R/x => R = (12/13)·x.
В треугольнике СНО SinС = R/(28-x) => R = (12/15)·(28-x).
Тогда (12/13)·x = (12/15)·(28-x) => 28x = 364 => x = 13cм.
R = (12/13)·x = 12 см.