Предмет: Алгебра,
автор: LeraBat18
Выполнить определённый интеграл
Приложения:
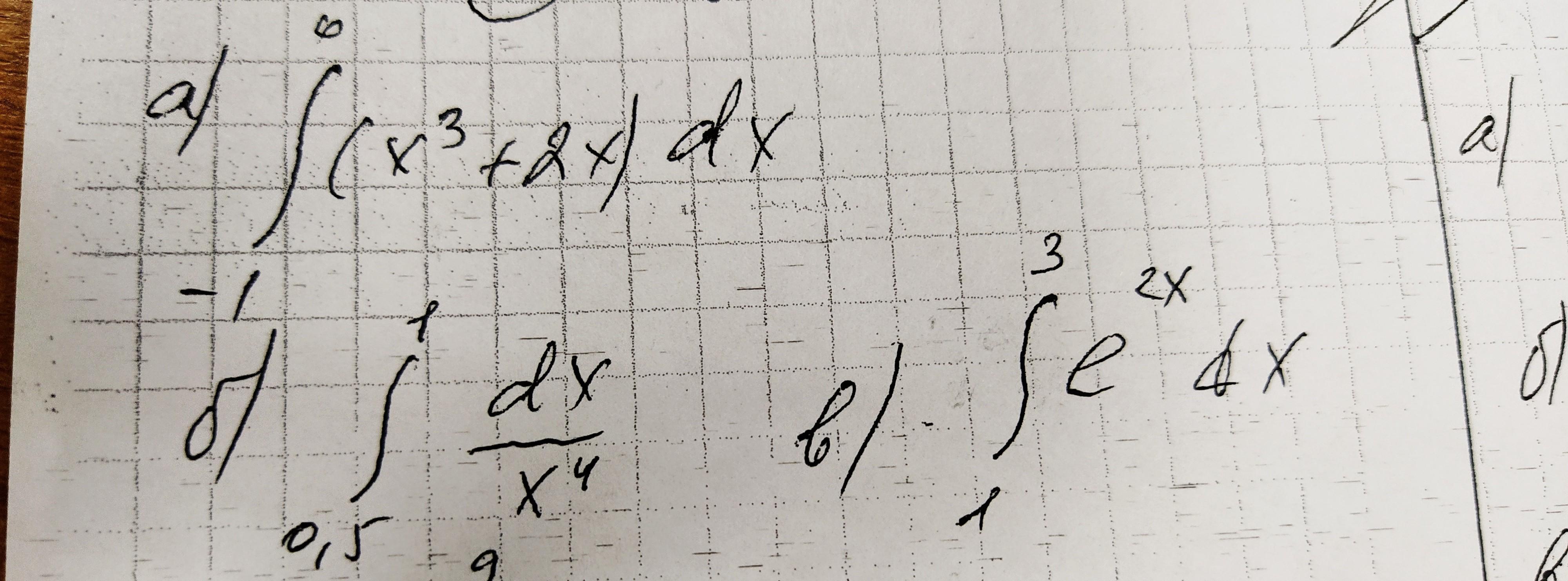
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: ohotnisa43
Предмет: Математика,
автор: meleshenkogalya1
Предмет: Українська література,
автор: aleksanderosypchukbc
Предмет: Математика,
автор: кук67