Предмет: Математика,
автор: Ksenia11064
Шар радиуса R=2440 км стянут по экватору крепким нерастяжимым обручем, плотно прилегающим к поверхности шара. Длину обруча увеличили на 43 сантиметра. Определите, пройдет ли в образовавшийся зазор хорошо накаченный мяч, длина окружности которого равна 8,26 дюйма. Примите π≈3,14, 1 дюйм=2,54 см.
а) в случае концентрического расположения обруча и шара; б) в случае, когда обруч касается поверхности шара.
Ответы
Автор ответа:
13
Пошаговое объяснение:
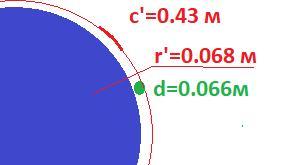
Рисунок к задаче в приложении.
Простое решение ВНИЗУ.
Длина экватора по формуле:
С = 2*π*R = 2*3.14*2440000 = 15 323 200 м
Прибавим 43 см = 0,43 м и найдем новый диаметр
С2 = 15323200,43 - длина обруча
R2 = C2: (2*3.14) = 2440 000.068 м
Зазор между обручами = 0,068 м = 6,8 см
Длина окружности мяча = с = 8,26 * 2,54 = 20,98 см
Диаметр мяча d =c /π = 20.98 : 3.14 = 6.68 см = 0,0668 м
И он пролезает - да и зазор еще есть.
х = 6,8 - 6,668 = 0,132 см - зазор - ответ.
ХИТРОСТЬ задачи, что сам размер радиуса Земли и не надо применять.
Прибавленные 43 см к обручу увеличат его радиус на
dR = 0.43 : (2*3.14) = 0.684 м, а диаметр мяча - расчет выше - 0,668.
Приложения:
dallon:
а что получается под а) и б)? да или нет?
а что получается под а) и б)? да или нет?
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: aolefirenkokf
Предмет: Математика,
автор: almirasd
Предмет: Обществознание,
автор: Минаханум
Предмет: Математика,
автор: ЭмильZharasov