Question

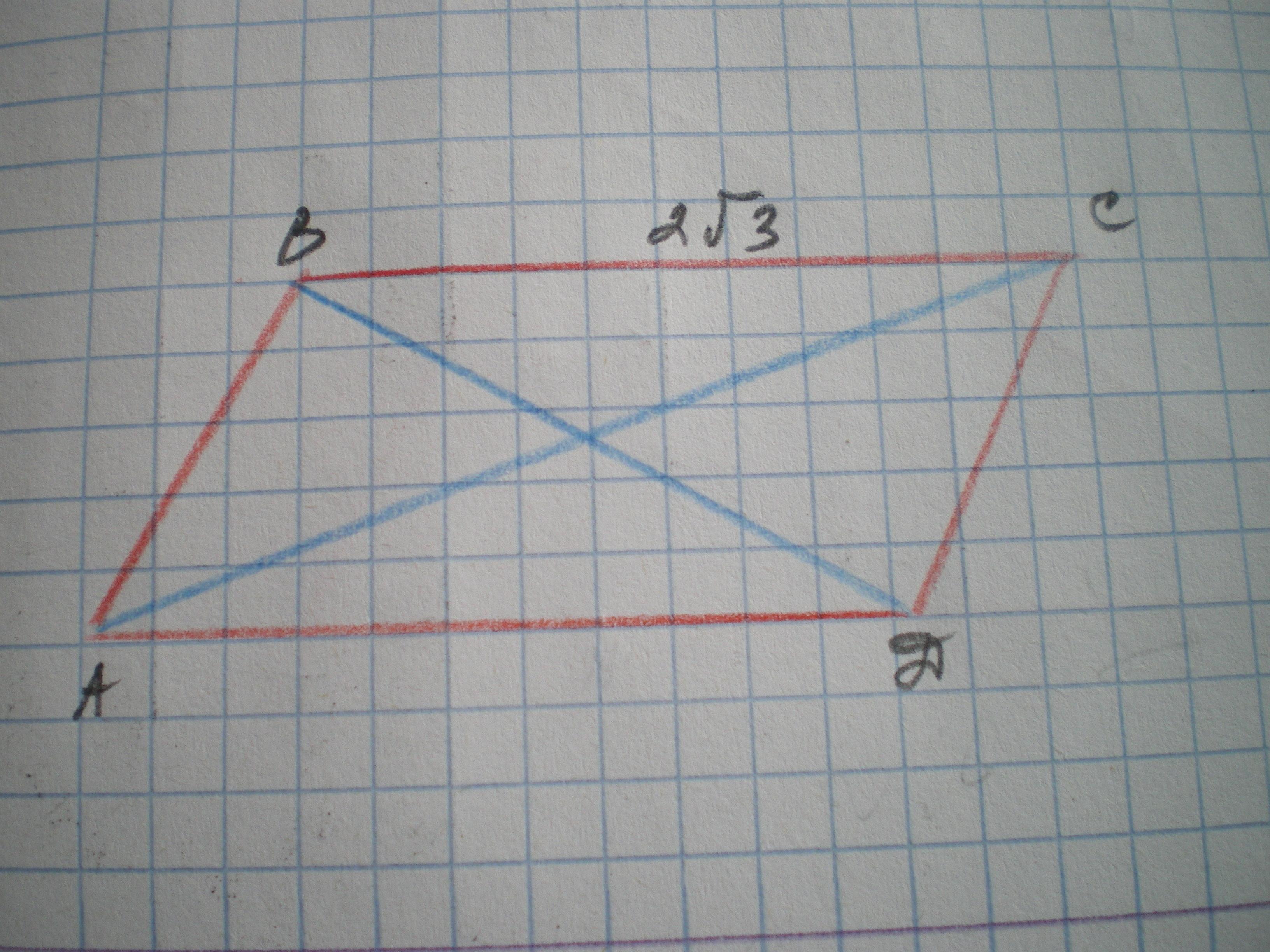
В параллелограмме АВСД диагонали равны 5см и 7см. Вычислите сторону АВ, если еслиВС 2корень из 3 см

Answer 1

Ответ:

5 см

Объяснение:

Дано: АВСD - параллелограмм, АС=7 см, BD=5 cм, ВС=2√3 см

Найти АВ.

Решение:

Сумма  квадратов диагоналей параллелограмма равна удвоенной сумме квадратов смежных сторон.

АС² + ВD² = 2(ВС² + АВ²)

7² + 5² = 2(2√3)² + 2АВ²

49 + 25 = 24 + 2АВ².  

2АВ² = 50;  АВ²=25.  

АВ = 5 см.

Answer 2

$AC=7\; ,\; BD=5\; ,\; BC=2\sqrt3$

Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

$AC^2+BD^2=AB^2+BC^2+CD^2+AD^2\\\\AB=CD\; ,\; \; BC=AD\\\\AC^2+BD^2=2\cdot (AB^2+BC^2)\\\\7^2+5^2=2\cdot (AB^2+(2\sqrt3)^2)\\\\49+25=2\cdot (AB^2+12)\\\\74=2\cdot (AB^2+12)\\\\AB^2+12=\frac{74}{2}\\\\AB^2=37-12\\\\AB^2=25\\\\AB=5$