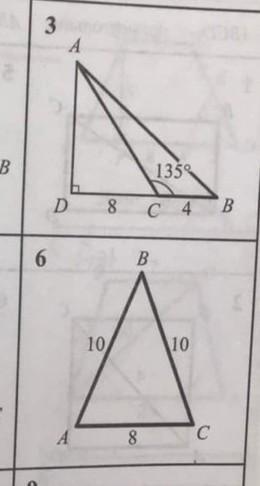
Найти площадь треугольника ABC. (оба треугольника)
Ответы
номер 3
1)угол ACD+ угол ACB =180 т.к они смежные, значит
угол ACD = 180- угол ACB = 180° -135° =45°
2)Рассмотрим треугольник ACD
по теореме о сумме углов треугольника:
угол ADC+угол DCA + угол CAD=180°, значит
угол CAD=180-угол ADC-угол DCA=180°-90°-45°=45°
3)угол DCA =угол CAD, значит треугольник ADC р.б поэтому AD=DC=8
4)S трADB =1/2 * a *h
S трADB=1/2 * AD * DB
SтрADB=1/2 * 8 * 12= 48
номер 6
1)треугольник ABC р.б т.к AB=BC
2)проведем медиану BD, медиана будет является также и высотой и биссектрой, значит AD=DC=4 и треугольники ABD и BDC прямоугольные (углы ADB и CDB равны 90°)
3)Рассмотрим треугольник ABD ,
по теореме Пифагора:
AD^2+BD^2=AB^2;
4^2+BD^2=10^2
16+BD^2=100
BD^2=84
BD=2√21
S трABC =1/2 * a *h
S трABC=1/2 * AC * DB
SтрABC =1/2 * 8 * 2√21= 8√21