Предмет: Алгебра,
автор: Mr0leg
Вычислить пределы, два номера
Приложения:
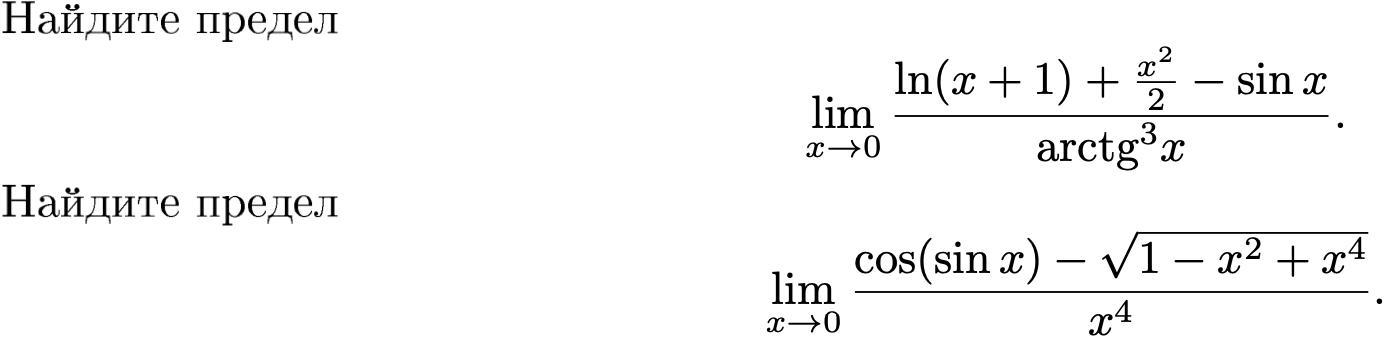
Ответы
Автор ответа:
1
В первом в знаменателе а в числителе будем каждую элементарную функцию разложить в ряд Тейлора
Аналогично решаем и со вторым примером.
Похожие вопросы
Предмет: Математика,
автор: yanderecan801
Предмет: Алгебра,
автор: marianna198722
Предмет: Алгебра,
автор: taejen21
Предмет: История,
автор: дракула52
Предмет: Физика,
автор: dersk1111y