Предмет: Алгебра,
автор: yelol
Найти область сходимости ряда
Приложения:
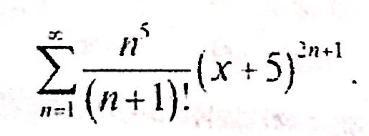
Ответы
Автор ответа:
2
Ответ:
Зафиксируем x.
А значит ряд сходится по признаку Д'Аламбера для любого фиксированного x. А значит область сходимости
Похожие вопросы
Предмет: Алгебра,
автор: Ggosudgdx8
Предмет: Русский язык,
автор: savcukmisa02
Предмет: Українська література,
автор: daraoprisan654
Предмет: Математика,
автор: mana345Natasz
Предмет: Математика,
автор: sonya271012004