Предмет: Алгебра,
автор: bertain
100 б + лучший ответ! Задание на фото.
Приложения:
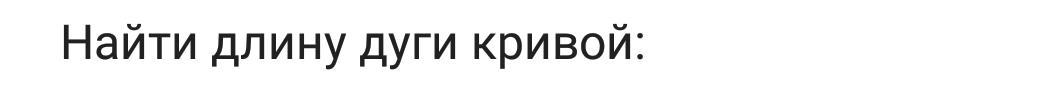
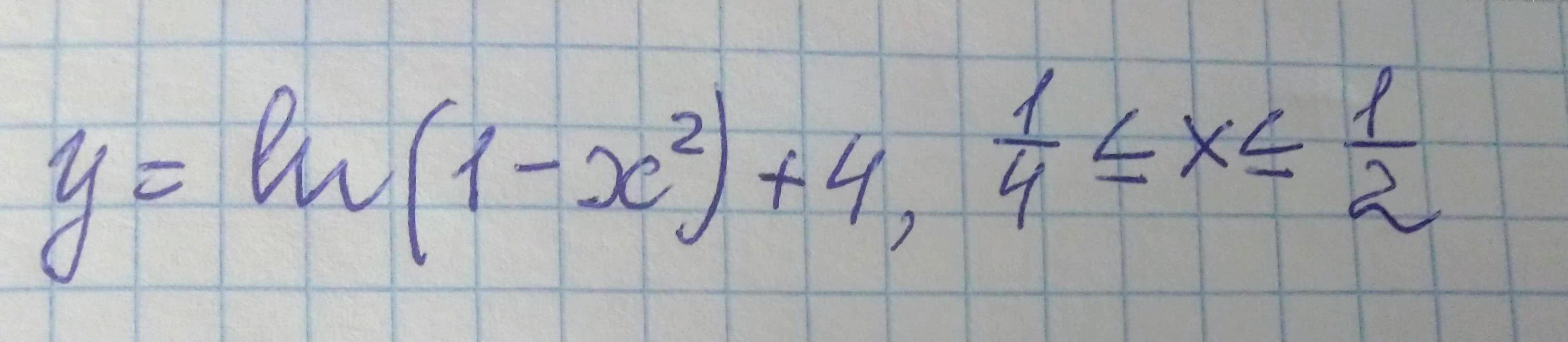
Ответы
Автор ответа:
1
Формула нахождение длины дуги кривой на отрезке [a;b]
Для данной задачи:
Поскольку длина не может быть отрицательной:
Ответ:
Автор ответа:
1
Ответ: во вложении Объяснение:
Приложения:
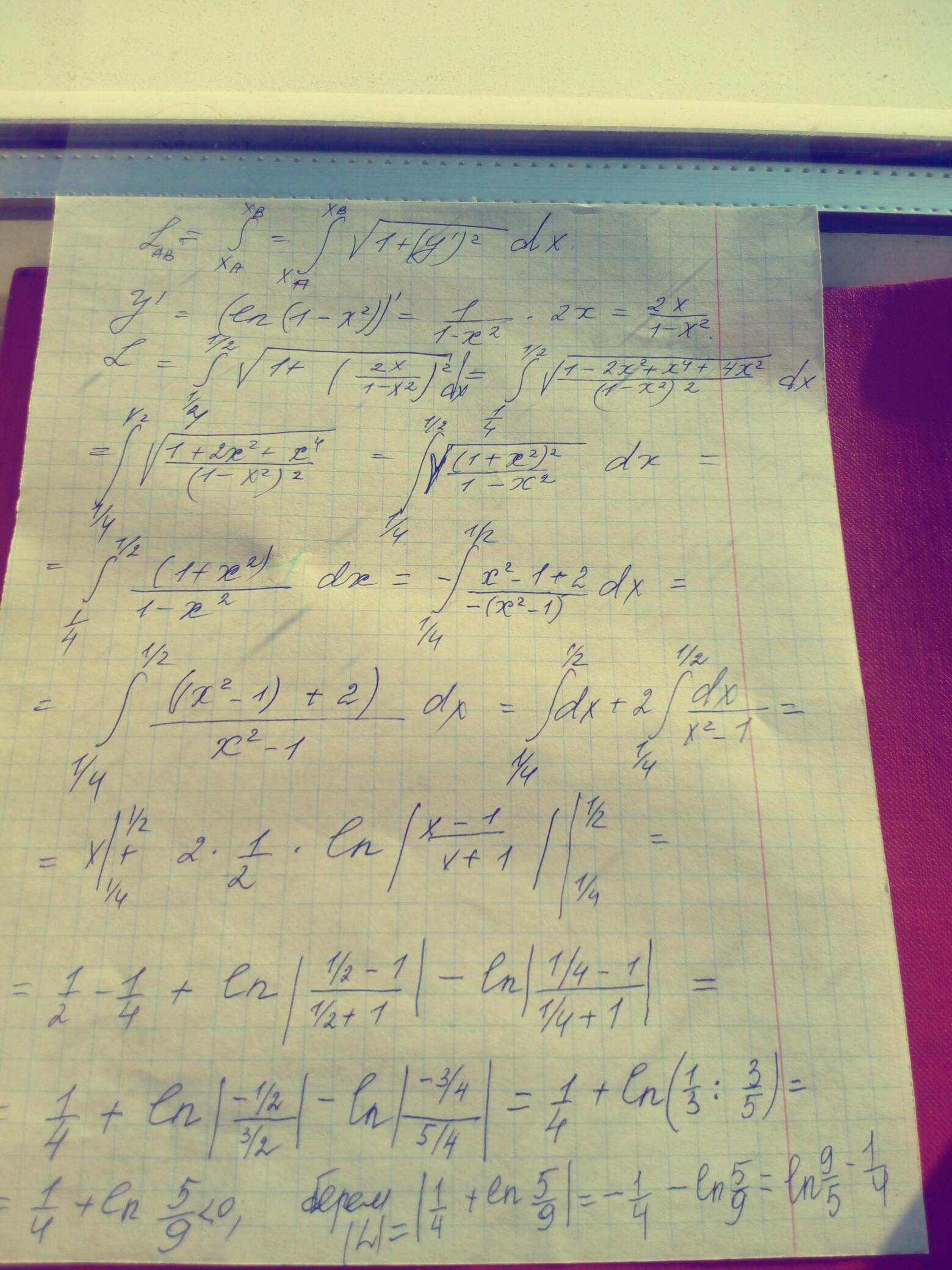
Похожие вопросы
Предмет: Математика,
автор: sokiranskakristina
Предмет: Математика,
автор: zaharikuk
Предмет: Литература,
автор: andrejkamardin278
Предмет: История,
автор: NikaUpiina984