Предмет: Алгебра,
автор: dinomidio
Решите систему уравнений

dinomidio:
+ ваши методы решения
Ответы
Автор ответа:
0
Решение задания приложено
Приложения:

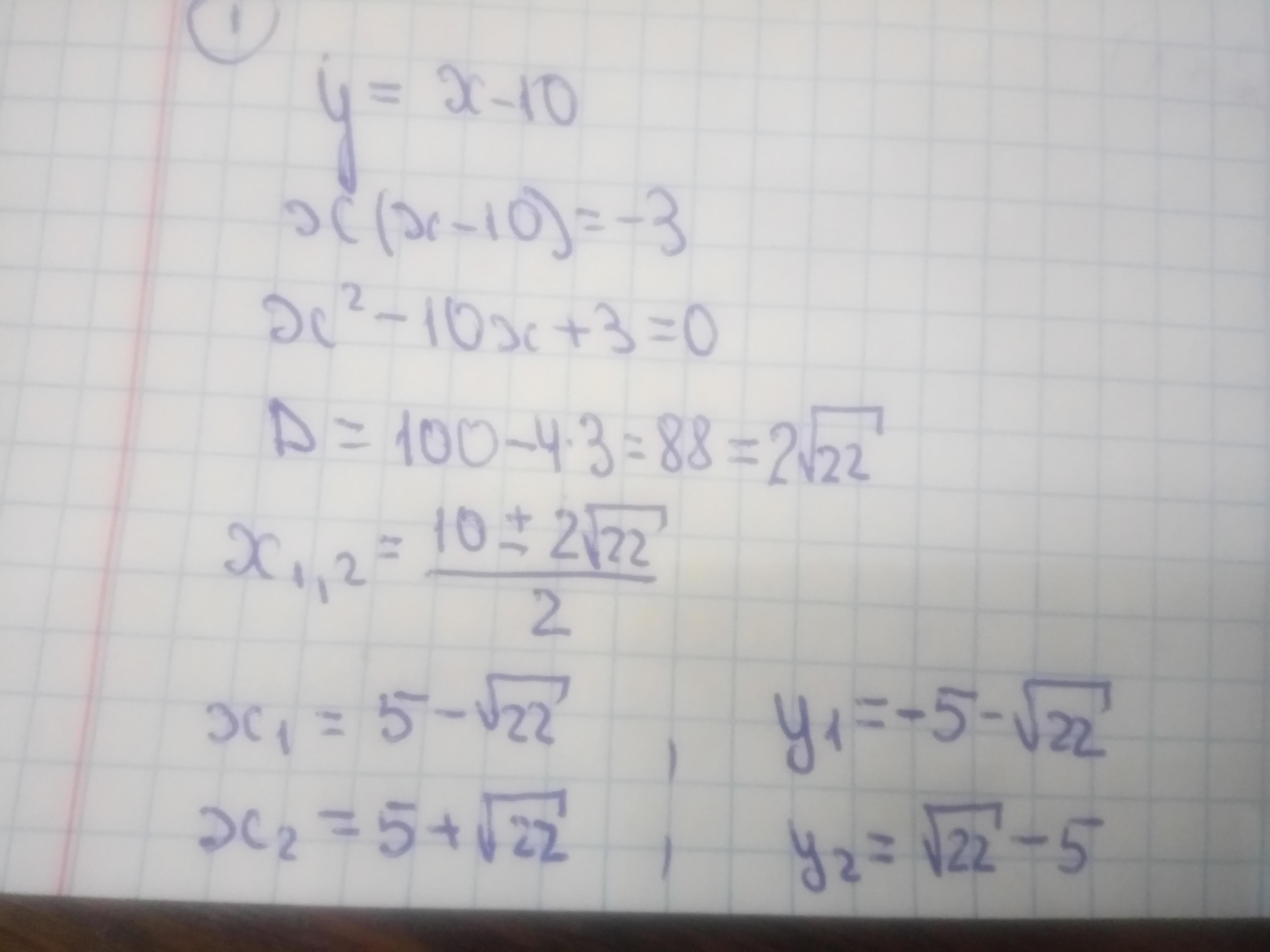

В запросе был выдан xy-x+y, у вас xy-y+x, в принципе тут другой пример
Автор ответа:
1
Объяснение:
обозначим xy=m; x-y=n
тогда получим
m и n корни квадратного уравнения
поэтому у системы два решения (m;n)=(10;-3) или же =(-3;10)
первое:
второе
Похожие вопросы
Предмет: Английский язык,
автор: dianakacanska
Предмет: Алгебра,
автор: crydears
Предмет: Литература,
автор: homenkomaksim222
Предмет: Литература,
автор: Wafli13