Question

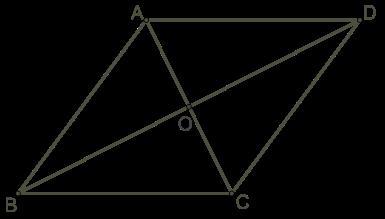
Дан ромб ABCD, точка O пересечения диагоналей AC и BD, короткая диагональ равна стороне ромба.

1) Угол между векторами DB−→− и DC−→− равен
°;

2) угол между векторами OB−→− и DO−→− равен
°;

3) угол между векторами AB−→− и CA−→− равен
°;

4) угол между векторами AD−→− и DB−→− равен
°;

5) угол между векторами CA−→− и DB−→− равен
°.

Answer 1

Ответ:

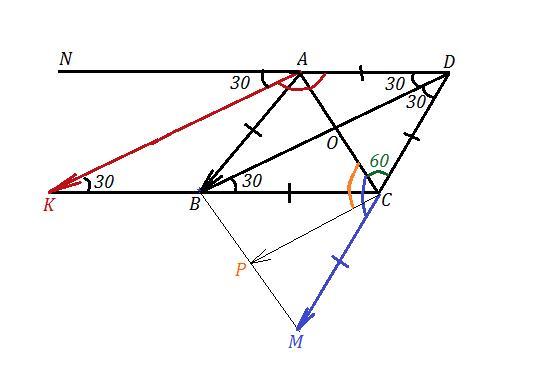
Так как короткая диагональ ромба АС равна его сторонам, то ΔАДС - равносторонний и все его углы = 60°. Диагонали ромба - биссектрисы его углов, поэтому  ∠АДС=∠СДВ=30° .

$1)\; \; \angle (\overline {DB}\, ,\, \overline {DC})=\angle CDB=30^\circ \\\\2)\; \; \angle (\overline {OB}\, ,\, \overline {DO})=0^\circ$

так как векторы коллинеарны (лежат на одной прямой) и сонаправлены

$3)\; \; AB\parallel CM\; \; \Rightarrow \; \; \angle (\overline {AB}\, ,\, \overline {CA})=\angle (\overline {CM}\, ,\, \overline {CA})=\angle ACM=\\\\=180^\circ -\angle ACD=180^\circ -60^\circ =150^\circ$

$4)\; \; DB\parallel AK\; \; \Rightarrow \; \; \angle (\overline {AD}\, ,\, \overline {DB})=\angle (\overline {AD}\, ,\, \overline {AK})=\angle DAK\; ,\\\\\angle DAK=180^\circ -\angle KAN\; ;\\\\\angle AKC=\angle DBC\; \; (AK\parallel DB\; ,\; KC\; -\; sekyshaya)\; ,\\\\\angle DBC=\angle BDC=30^\circ \; \; (\Delta BDC\; -\; ravnobedrennuj\; ,\; BC=DC)\; \; \Rightarrow \\\\\angle AKC=30^\circ \\\\\angle KAN=\angle AKC=30^\circ \; \; (KC\parallel AN\; ,\; AK\; -\; sekyshaya)\\\\\angle DAK=180^\circ -30^\circ =150^\circ$

$5)\; \; \angle (\overline {CA}\, ,\, \overline {DB})=90^\circ$ ,

так как это угол между диагоналями ромба.

Или  $CP\parallel DB$

$\angle (\overline {CA}\, ,\, \overline {DB})=\angle (\overline {CA}\, ,\, \overline {CP})=\angle ACP=180^\circ -\angle ACD-\angle MCP=\\\\=180^\circ -60^\circ -30^\circ =90^\circ$