Предмет: Геометрия,
автор: Anthony2003
У неправильного выпуклого четырёхугольника средние линии с длинами 10 и 20 пересекаются под углом 30 градусов. Найти площадь четырёхугольника.
siestarjoki:
Площадь параллелограмма Вариньона равна половине площади четырехугольника.
S= 1/2 *10*20 *1/2 *2 =100
Ответы
Автор ответа:
2
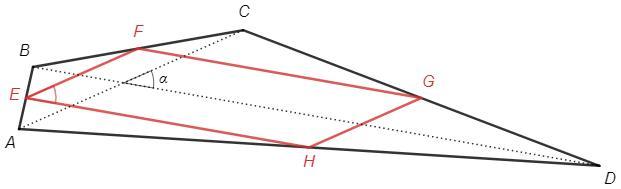
Середины сторон четырехугольника являются вершинами параллелограмма Вариньона (1).
Средние линии четырехугольника - диагонали параллелограмма Вариньона.
S(EFGH) = 1/2 *10*20 *sin30
Площадь параллелограмма Вариньона равна половине площади четырехугольника (2).
S(ABCD)= 2 S(EFGH) =100
1) EF - средняя линия ABC, EF||AC
Аналогично GH||AC, FG||BD, EH||BD
EFGH - параллелограмм
2) S(ABCD)= 1/2 AC*BD *sina
(a - угол между диагоналями)
E=a, EF=1/2 AC, EH=1/2 BD
S(EFGH) = EF*EH *sinE = 1/2 S(ABCD)
Приложения:

Похожие вопросы
Предмет: Алгебра,
автор: liq0ro
Предмет: Английский язык,
автор: krakennolik52
Предмет: Алгебра,
автор: PrivetAndrey12
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: школьные3