Предмет: Алгебра,
автор: dafgyhj
Даю 55 баллов, нужно развёрнутое решение
Приложения:
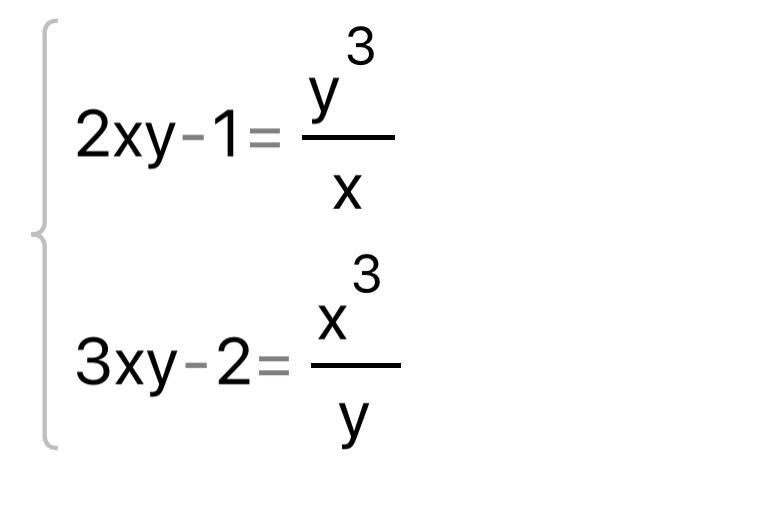
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Алгебра,
автор: ssssaasssha1803
Предмет: Русский язык,
автор: janetta2008
Предмет: Физкультура и спорт,
автор: rechyyy13
Предмет: Математика,
автор: аришка081