Question

СРОЧНО ПОМОГИТЕ!!!!!!!!!!!!!!!!!
ЗАРАНЕЕ СПАСИБО!

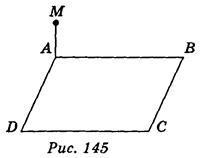
Дан прямоугольник ABCD, в котором АВ = 3 см, AD = 4 см, МА = 1 см. Отрезок МА перпендикулярен к плоскости АВС.


Пользуясь рисунком, найдите:


1) расстояние между точками М и В


2) длину отрезка MD


3) расстояние между точками А и С


4) длину отрезка BD


5) расстояние между точками М и С


6) площадь треугольника МAC

С ОБЪЯСНЕНИЕМ, ПОЖАЛУЙСТА, КАК ПОЛУЧИЛИСЬ ОТВЕТЫ

Answer 1

АВСД - прямоугольник  ⇒   ∠А=∠В=∠С=∠Д=90° .

Так как МА⊥ пл. АВСД  ⇒  МА ⊥АВ , МА⊥АД , МА⊥АС.

Тогда треугольники АВМ , АДМ, АСМ, АДС, АДВ - прямоугольные , и к ним можно применить теорему Пифагора.

$1)\; \; MB=\sqrt{AB^2+AM^2}=\sqrt{3^2+1^2}=\sqrt{10}\\\\2)\; \; MD=\sqrt{AD^2+AM^2}=\sqrt{4^2+1^2}=\sqrt{17}\\\\3)\; \; AC=\sqrt{AD^2+CD^2}=\sqrt{4^2+3^2}=5\\\\4)\; \; BD=\sqrt{AD^2+AB^2}=\sqrt{4^2+3^2}=5\; ,\; \; AC=BD\; .$

$5)\; \; CM=\sqrt{AC^2+AM^2}=\sqrt{5^2+1^2}=\sqrt{26}\\\\6)\; \; S(MAC)=\frac{1}{2}\cdot AC\cdot AM=\frac{1}{2}\cdot 5\cdot 1=2,5$