Предмет: Математика,
автор: Innak1225
Помоги решить. Найти предел функции
Приложения:
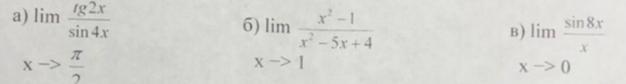
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Литература,
автор: polinapevenci
Предмет: Математика,
автор: Laokok
Предмет: Українська мова,
автор: emila3530
Предмет: Биология,
автор: u0276750
Предмет: История,
автор: ай23