Предмет: Алгебра,
автор: Lana2201
Найдите решение уравнения
Приложения:
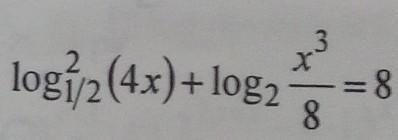
Ответы
Автор ответа:
1
Автор ответа:
1
Ответ: во вложении Объяснение:
Приложения:

Похожие вопросы
Предмет: Українська мова,
автор: yanabeharska
Предмет: Геометрия,
автор: zevws1
Предмет: Математика,
автор: milka456717
Предмет: Алгебра,
автор: Аноним
Предмет: Обществознание,
автор: migitkodmitrii