даю 30 баллов .решите хотя бы 2 задачи
Ответы
Решение данных задач основано на теореме Пифагора: Квадрат гипотенузы равен сумме квадратов катетов.
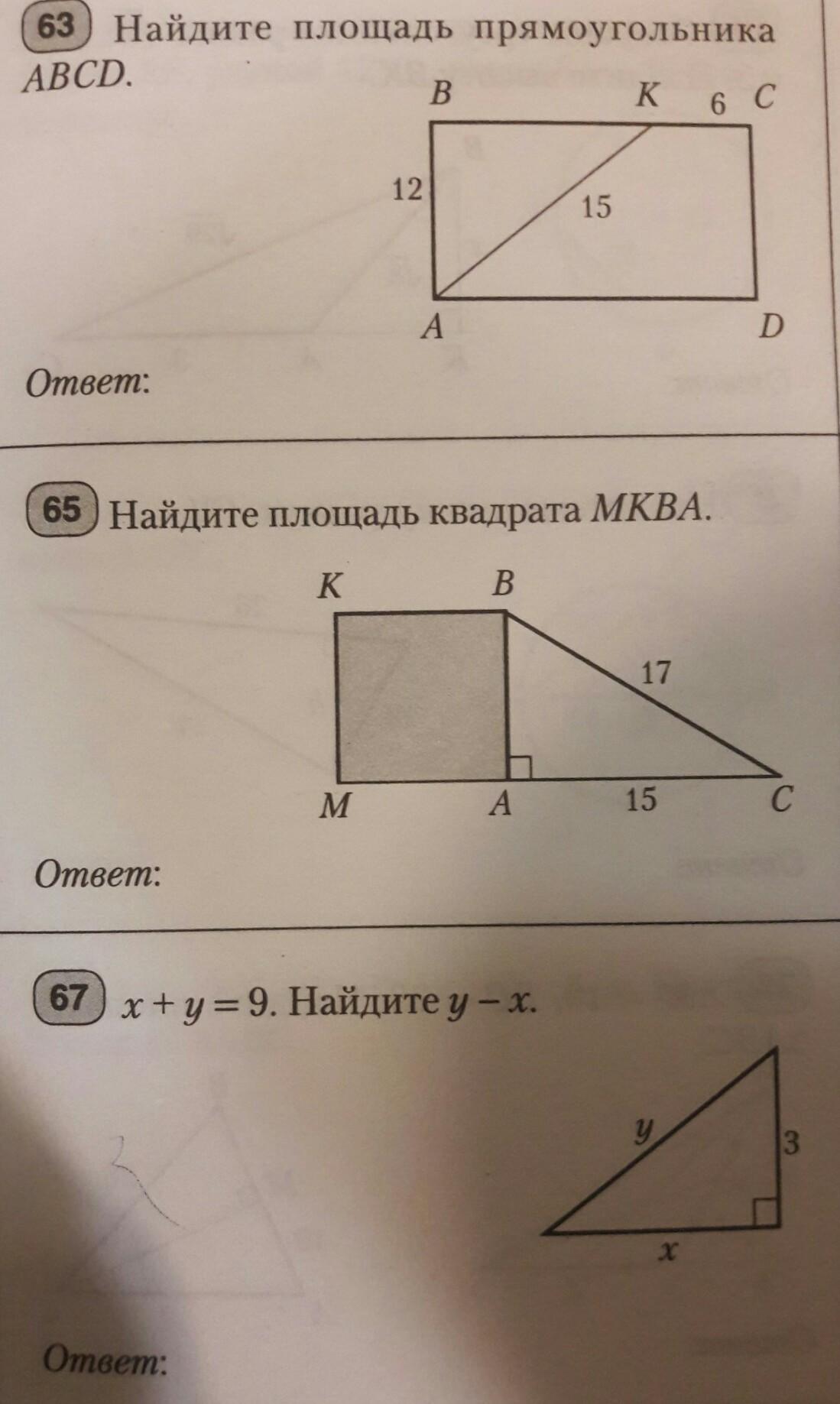
№ 63 Найдите площадь прямоугольника АВСD
Δ АВК - прямоугольный, так угол В - угол прямоугольника по условию
ВК = √(АК² - АВ²) = √(15² - 12²) = √(225 - 144) = √89 = 9
ВС = ВК + КС = 9 + 6 = 15
S(АВСD) = АВ * ВС = 12 * 15 = 180 (кв.ед.)
Ответ: 180 кв.ед.
№ 65 Найдите площадь квадрата МКВА
Так как Δ АВС - прямоугольный по условию, то АВ² = ВС² - АС² = 17² - 15² = 289 - 225 = 64
Так как МКВА - квадрат по условию, то S(МКВА) = АВ² = 64 (кв.ед.)
Ответ: 64 кв.ед.
№ 67 х + у = 9 . Найдите у = х
Δ на рисунке - прямоугольный.
у² - х²= 3²
Разложим у² - х² по формуле разности квадратов
(у - х)*(у + х) = 9
Но по условию х + у = 9, тогда
(у - х) * 9 = 9
у - х = 9 : 9 = 1
Ответ: у - х = 1