Предмет: Алгебра,
автор: elionora456
Помогите пожалуйста алгебра номер 8.22.
Приложения:
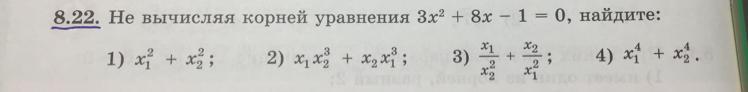
Ответы
Автор ответа:
6
Похожие вопросы
Предмет: Математика,
автор: Gpr00
Предмет: Право,
автор: annatisenko225
Предмет: Английский язык,
автор: pavliva0050
Предмет: Математика,
автор: снежинка289
Предмет: Математика,
автор: Маша211598