Question

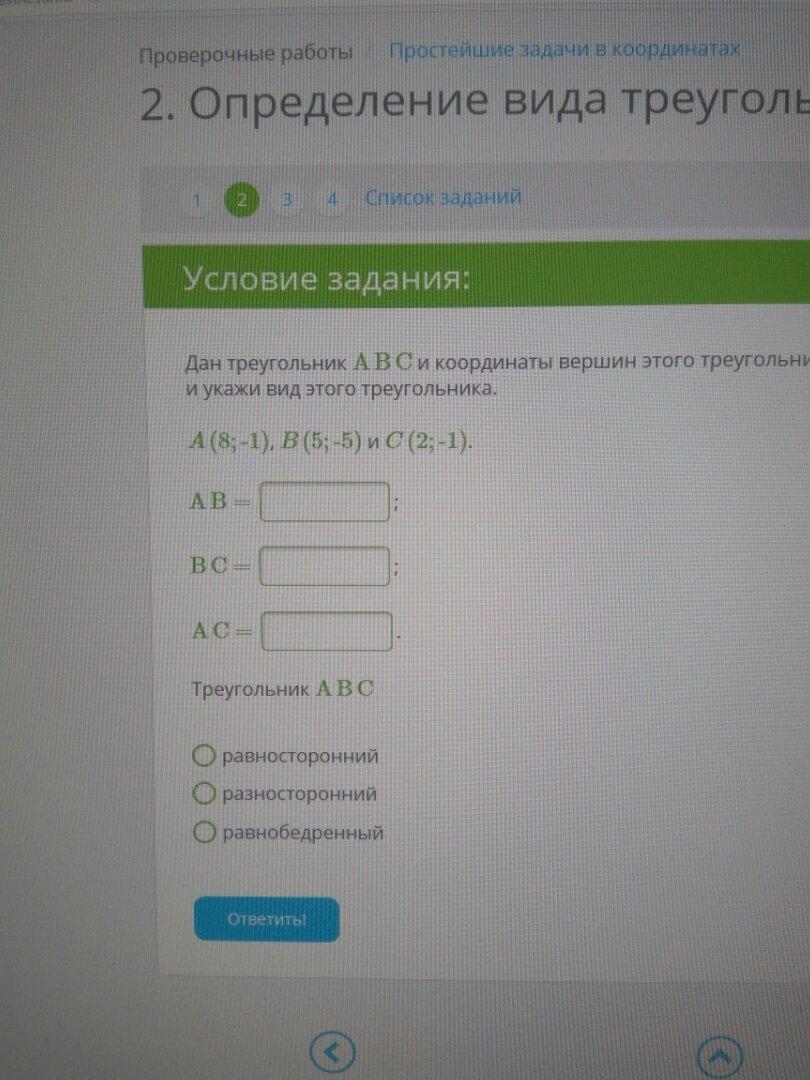
Дан треугольник ABC и координаты вершин этого треугольника. Определи длины сторон треугольника иукажи вид этого треугольника. A(8;-1), B(5;-5)и C(2;-1).

Answer 1

AB =(5-8)^2+(-5+1)^2 = 9+16 = 5

BC = (2-5)^2+(-1+5)^2 = 9+16 =5

AC = (2-8)^2+(-1+1)^2 = 6

Т.к. AB=BC

следовательно треугольник ABC равнобедренный

Пошаговое объяснение:

Все эти выражения под корнем !

Как я находил числа:

AB = корень из (x2-x1)^2 + (y2-y1)^2

Плз лучший ответ