Предмет: Математика,
автор: ainurbailina
Найдите точки пересечения графиков функций
Приложения:
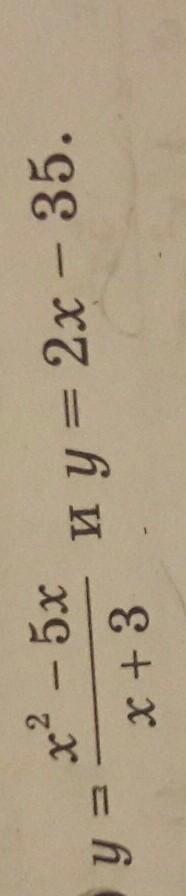
Ответы
Автор ответа:
1
Ответ:
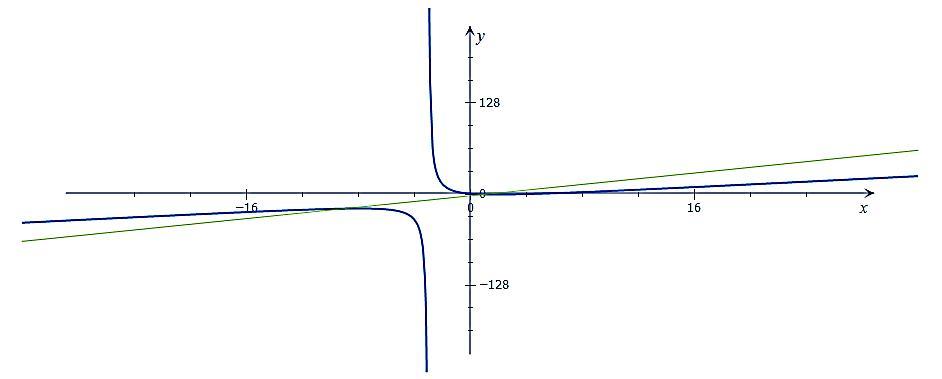
Точки пересечения графиков функций
Пошаговое объяснение:
Для определения точек пересечения графиков (см. рисунок) функций и
приравниваем их и решаем уравнение:
D=(-24)²-4·1·(-105)=576+420=996
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: anjelakuzmina8
Предмет: Алгебра,
автор: ssamsungi491
Предмет: Английский язык,
автор: loshka34354
Предмет: История,
автор: яэтомы
Предмет: Математика,
автор: Юну1